Come creare una matrice sparsa con i numeri complessi su Octave

In questa lezione ti spiego come creare una matrice sparsa con i numeri complessi su Octave.

Ti faccio un esempio pratico.

Ad esempio, crea una matrice sparsa con questi valori.

$$ M = \begin{pmatrix} 3+2i & 0 & 4+5i \\ 0 & 1+3i & 2-4i \\ 4+i & 0 & 0 \end{pmatrix} $$

La matrice ha 5 elementi non nulli.

Definisci un array con cinque righe, una riga per ciascun elemento non nullo della matrice.

>> v = [1 1 3 2; 1 3 4 5; 2 2 1 3; 2 3 2 -4; 3 1 4 1]
v =
1 1 3 2
1 3 4 5
2 2 1 3
2 3 2 -4
3 1 4 1

In ciascuna riga dell'array scrivi queste informazioni nel seguente ordine

• il numero di riga della matrice
• il numero di colonna della matrice
• la parte reale del numero complesso
• la parte immaginaria del numero complesso.

Complessivamente l'array ha sempre 4 colonne e un numero di righe uguale al numero degli elementi non nulli della matrice.

Spiegazione. Nella prima riga e colonna (1,1) della matrice si trova il numero complesso 3+2i. La parte reale del numero complesso è 3, quella immaginaria è 2. Per rappresentare questo elemento della matrice devi indicare nell'array una riga con i valori 1 1 3 2. E via dicendo.

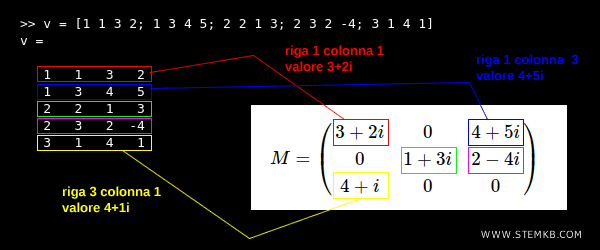
Per definire gli elementi della matrice puoi seguire qualsiasi ordine. Ad esempio, Puoi definire prima l'elemento (2,2) e poi (1,1) o viceversa. Il risultato finale è lo stesso.

Una volta definito il vettore, crea la matrice sparsa usa usando la funzione spconvert()

>> spconvert(v)

La funzione spconvert() converte un array di 3 o 4 colonne in una sparse matrix.

Il risultato è una matrice sparsa con i numeri complessi nelle posizioni che hai indicato.

ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 5 [56%])

(1, 1) -> 3 + 2i
(3, 1) -> 4 + 1i
(2, 2) -> 1 + 3i
(1, 3) -> 4 + 5i
(2, 3) -> 2 - 4i

Quando definisci l'array degli elementi puoi anche associare più valori a una stessa posizione (riga,colonna) della matrice.

In questi casi Octave somma automaticamente i valori tra loro.

Esempio. Definisci una matrice sparsa indicando nella posizione (1,1) prima il numero 2+3i e poi il numero 3+4i. Octave somma i due numeri complessi tra loro (2+3i)+(3+4i)=5+7i e li scrive nella posizione (1,1) della matrice sparsa.

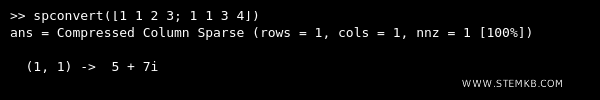
Se questa lezione di StemKB ti ha aiutato, continua a seguirci.