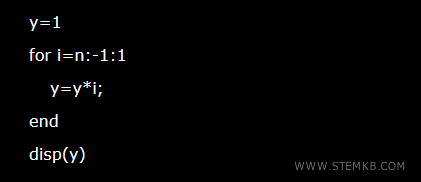Le funzioni ricorsive su Octave
In questa lezione ti spiego come usare la ricorsione nelle funzioni su Octave
Cos'è la ricorsione? Una funzione si dice ricorsiva se richiama se stessa più volte. E' alla base della programmazione funzionale.
Ti faccio un esempio pratico.
Puoi usare la ricorsione per calcolare il fattoriale di un numero.
1;
function y = fact(x)
if (x<0)
disp("numero negativo")
return;
endif
if (x<2)
y=1;
return;
else
y=x*fact(x-1)
endif
endfunction
In questo script ho definito una funzione fact() che riceve un numero in entrata (x)
- Se x<0
Se il numero è negativo la funzione si limita a dire che il numero è negativo e non fa più nulla perché il fattoriale di un numero negativo non può essere calcolato. L'istruzione return termina anticipatamente l'esecuzione della chiamata di funzione.

- Se 0≤x<2
Se il numero è minore di 2 la funzione restituisce 1 e termina la ricorsione. L'istruzione return restituisce il valore 1 alla precedente chiamata di funzione. Il processo torna indietro cominciando a chiudere le precedenti chiamate ricorsive.

- Se x≥2
In tutti gli altri casi il numero è maggiore di 1. In questi casi la funzione moltiplica il numero x per il risultato della funzione fact(x-1). Quindi, la funzione richiama se stessa (ricorsione) con una nuova chiamata della funzione fact(x-1). Dove x-1 è il numero intero corrente (x) ridotto di uno (-1).

Ad esempio, richiama la funzione fact() che hai appena creato passando 6 come parametro iniziale.
La funzione riceve in ingresso il numero x=6 e calcola ricorsivamente il fattoriale.
n=6
y=fact(n);
disp(y)
Lo script restituisce in uscita il numero 720 ossia il fattoriale di 6!
720
Perché l'output della funzione è 720?
La funzione richiama se stessa cinque volte (ricorsione) passando un numero via via inferiore.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)
Nell'ultima chiamata fact(1)=1 la funzione restituisce 1 perché il valore in ingresso (x=1) è minore di due
A questo punto la ricorsione termina e il processo torna indietro chiudendo man mano tutte le chiamate precedenti
Se fact(1)=1 allora fact(2)=2 perché fact(2)=2*fact(1)=2*1=2
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2
Se fact(2)=2 allora fact(3)=6 perché fact(3)=3*fact(2)=3*2=6
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)=3*2=6
Se fact(3)=6 allora fact(4)=24 perché fact(4)=4*fact(3)=4*6=24
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)=4*6=24
Se fact(4)=24 allora fact(5)=120 perché fact(5)=5*fact(4)=5*24=120
fact(6)=6*fact(5)
fact(5)=5*fact(4)=5*24=120
Se fact(5)=120 allora fact(6)=720 perché fact(6)=6*fact(5)=6*120=720
fact(6)=6*fact(5)=6*120=720
Pertanto il fattoriale di 6! è 120
$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$
Nota. In questo esempio ho creato una funzione fattoriale per spiegarti come funziona la ricorsione in Octave. Tuttavia, se la tua esigenza è solo quella di calcolare il fattoriale ricorda che Octave ha anche una funzione specifica predefinita. Si tratta di factorial(x). E' molto più comoda da usare. Inoltre, puoi calcolare il fattoriale anche sviluppando una funzione basata sull'iterazione senza usare la ricorsione. Il risultato è sempre lo stesso.