Come calcolare la somma superiore di un integrale

In questa lezione ti spiego come calcolare con un'approssimazione per eccesso l'integrale di una funzione su Geogebra.

Ti faccio un esempio pratico.

Disegna il grafico di una funzione tramite una espressione matematica oppure a mano libera.

Geogebra assegna automaticamente un nome alla funzione. Ad esempio f(x)

Digita nel pannello di Geogebra il comando SommaSuperiore()

• Il primo parametro è il nome della funzione. Ad esempio f(x)
• Il secondo e il terzo parametro sono gli estremi dell'integrazione. Ad esempio, usa l'intervallo (-3,2) della variabile indipendente x.
• Il quarto parametro è il numero di rettangoli con cui vuoi dividere l'intervallo ossia la partizione dell'intervallo. Ad esempio, 10 rettangoli.

Questo comando di Geogebra visualizza una partizione dell'intervallo con 10 rettangoli.

La somma dell'area dei 10 rettangoli è detta somma superiore e approssima per eccesso l'area sottesa alla funzione.

In questo caso l'area sotto il grafico della funzione è circa 18.83

Nota. Si tratta di un'approssimazione per eccesso. In realtà, l'area sotto il grafico della funzione è inferiore a 18.83. Per avere un valore più preciso calcola anche la somma inferiore oppure l'integrale definito della funzione nello stesso intervallo (-3,2).

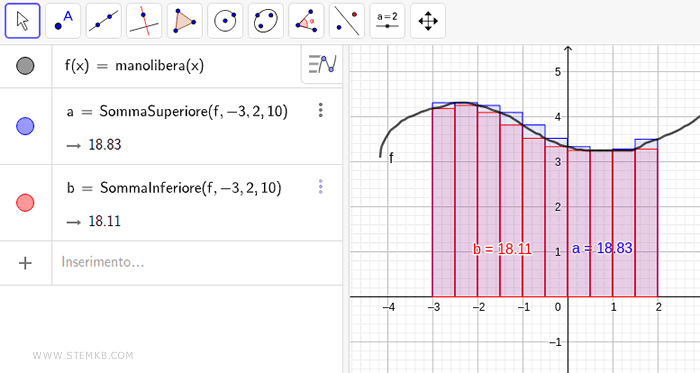
Una volta calcola sia la somma inferiore che la somma superiore puoi affermare con certezza che l'integrale è compreso tra 18.11 e 18.83. L'integrale coincide con l'area sottesa se la funzione nell'intervallo è sempre positiva.

Se questa lezione breve di StemKB è utile e ti ha aiutato, continua a seguirci.