La norma o modulo di un vettore su Geogebra

In questa lezione ti spiego come calcolare il modulo (lunghezza o norma) di un vettore usando GeoGebra.

A cosa serve la norma? La norma di un vettore rappresenta la sua lunghezza, ovvero la distanza del punto terminale dall’origine. È utile per confrontare vettori, per normalizzarli (cioè renderli unitari), o per calcolare angoli tra vettori tramite il prodotto scalare.

Partiamo dalla creazione di un vettore. Puoi lavorare nel piano oppure nello spazio tridimensionale: GeoGebra funziona in entrambi i casi.

Un vettore nel piano

Supponiamo di voler calcolare la norma del seguente vettore:

\[ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} \]

Se non ti ricordi come inserire un vettore in GeoGebra, puoi consultare la lezione sui vettori nel piano cartesiano.

Per creare il vettore in GeoGebra, puoi scrivere nel campo di inserimento:

v = Vector((0, 0), (3, 4))

Questo comando crea un vettore \( \vec{v} \) che parte dall'origine e termina nel punto (3, 4).

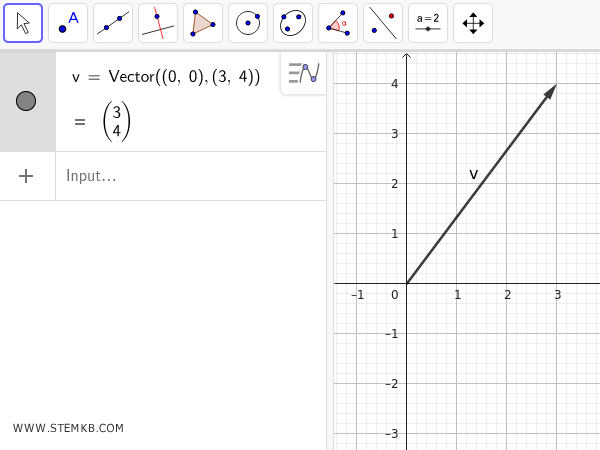
Ora per calcolare la norma (o modulo) del vettore, scrivi nel campo di inserimento il comando Length() indicando tra le parentesi tonde il nome del vettore:

Length(v)

GeoGebra calcola e ti restituisce la norma del vettore che in questo caso è 5.

5

Dal punto di vista geometrico è la distanza tra il punto terminale del vettore e l'origine degli assi.

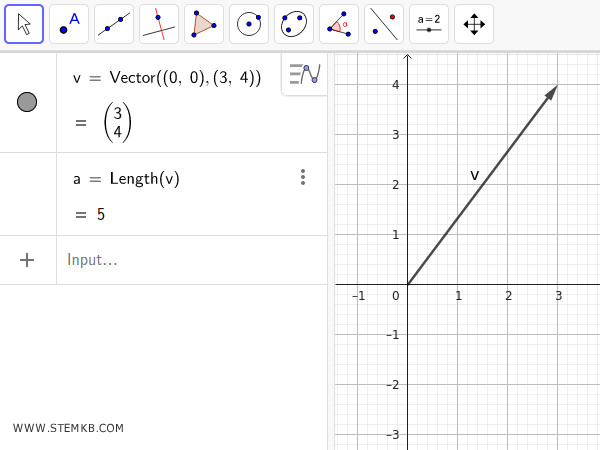
Se vuoi verificare, il valore restituito è proprio il valore del modulo del vettore calcolato con la formula matematica:

\[ \|\vec{v}\| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]

Un vettore nello spazio

Se invece vuoi lavorare nello spazio a tre dimensioni, puoi inserire un vettore come questo:

\[ \vec{u} = \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix} \]

Vai su Geogebra e digita:

u = (2, -1, 2)

Poi calcola la norma con il comando Lenght().

Length(u)

GeoGebra ti restituirà la norma, ossia la lunghezza, del vettore nello spazio 3D

3

Anche in questo caso il risultato è la lunghezza del vettore che, in questo caso, è nello spazio tridimensionale.

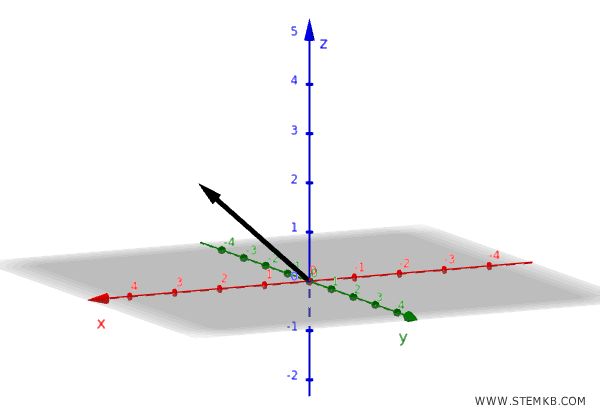
E' lo stesso valore che ottieni calcolando manualmente la norma del vettore.

\[ \|\vec{u}\| = \sqrt{2^2 + (-1)^2 + 2^2} = \sqrt{4 + 1 + 4} = \sqrt{9} = 3\]

La norma di un vettore con più di tre dimensioni

GeoGebra non consente di definire vettori con più di 3 componenti come oggetti geometrici veri e propri.

Questo significa che non puoi creare vettori nello spazio a 4 dimensioni (o superiori) tramite i comandi classici come Vector(), né visualizzarli graficamente.

Tuttavia, puoi comunque calcolare manualmente il modulo (norma) di un vettore con più di tre componenti usando il campo CAS o l'algebra, ad esempio scrivendo direttamente:

sqrt(1^2 + 2^2 + 3^2 + 4^2)

oppure, se usi una lista e poi sommi i quadrati degli elementi della lista:

v := {1, 2, 3, 4}
sqrt(Sum(v^2))

In questi casi, GeoGebra funziona come una calcolatrice simbolica, utile per eseguire i calcoli anche se non tratta la lista come un vero vettore geometrico.

Se questa guida pratica di StemKB ti è stata utile, continua a seguirci per altre lezioni su GeoGebra e la matematica visuale.