Il prodotto vettoriale su Geogebra

In questa lezione ti spiego come fare il prodotto vettoriale di due vettori su Geogebra.

Crea due vettori nello spazio a tre dimensioni.

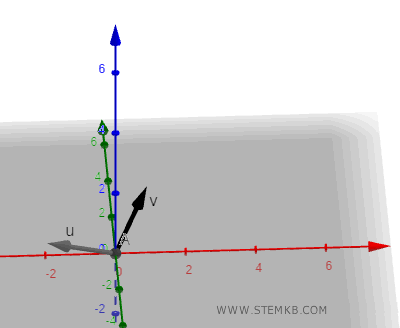
Il primo vettore ha le coordinate

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} $$

Il secondo vettore ha le coordinate

$$ \vec{u} = \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix} $$

Se non ricordi come fare un vettore puoi vedere quest'altra lezione online dedicata ai vettori su Geogebra.

Ora digita Cross(v,u) in un nuovo campo di Geogebra e dai invio.

Dove u e v sono i nomi dei due vettori che hai appena creato.

Geogebra calcola e visualizza il prodotto vettoriale dei due vettori.

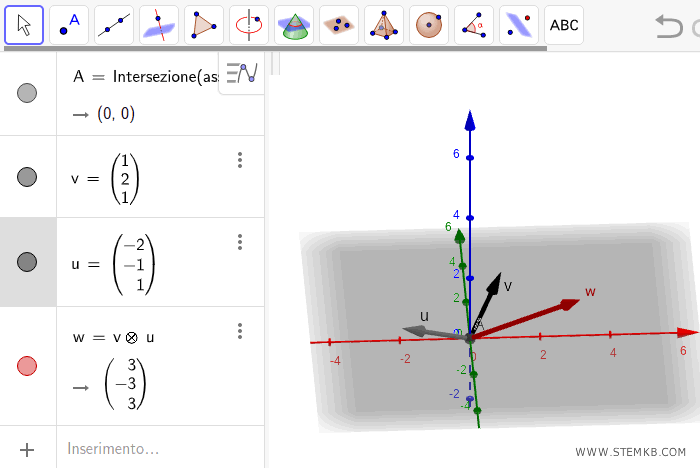
In questo caso il prodotto vettoriale è il vettore w che ha le seguenti coordinate.

$$ \vec{u} = \begin{pmatrix} 3 \\ -3 \\ 3 \end{pmatrix} $$

A cosa serve il prodotto vettoriale? Il prodotto vettoriale di due vettori u e v è un altro vettore w che ha la caratteristica di trovarsi in una direzione perpendicolare a entrambi i due vettori. Il verso del prodotto vettoriale dipende dall'ordine dei vettori. Nel caso particolare in cui i due vettori hanno la stessa direzione, il prodotto vettoriale è un vettore nullo. La lunghezza (modulo) del prodotto vettoriale corrisponde all'area formata dai due vettori sul piano che hanno in comune.

Se questa guida pratica di StemKB ti piace, continua a seguirci.