Il moto rettilineo uniformemente accelerato
Il moto rettilineo uniformemente accelerato è un tipo di moto in cui un corpo si muove lungo una linea retta con un'accelerazione costante.
La velocità del corpo aumenta linearmente nel tempo, partendo da una velocità iniziale.
La posizione del corpo cambia secondo una legge quadratica rispetto al tempo.
Vediamo di spiegare il concetto del moto rettilineo uniformemente accelerato in modo semplice e con esempi pratici.
Legge della posizione
La formula per la posizione in un moto uniformemente accelerato è:
\[ s = s_0 + v_0 t + \frac{1}{2} a t^2 \]
Questa formula dice che la posizione in un dato momento (s) è uguale alla posizione iniziale (\(s_0\)) più il prodotto della velocità iniziale (\(v_0\)) e il tempo trascorso (t), più mezzo prodotto dell'accelerazione (a) e il quadrato del tempo (t²).
Dove:
- \( v \) è la velocità in un istante qualsiasi.
- \( v_0 \) è la velocità iniziale (velocità all'inizio, quando t = 0).
- \( t \) è il tempo trascorso.
- \( a \) è l'accelerazione costante (quanto velocemente cambia la velocità nel tempo).
- \( s_0 \) è la posizione iniziale (posizione all'inizio, quando t = 0).
- \( s \) è la posizione in un istante qualsiasi.
Se la posizione iniziale e la velocità iniziale sono entrambe zero (\(s_0 = 0\) e \(v_0 = 0\)) la formula della posizione si semplifica. La posizione sarà $$ s = \frac{1}{2} a t^2 $$
Legge della velocità
La formula per la velocità in un moto uniformemente accelerato è:
\[ v = v_0 + at \]
Questa formula dice che la velocità in un dato momento (v) è uguale alla velocità iniziale (\(v_0\)) più il prodotto dell'accelerazione (a) e del tempo trascorso (t).
Se la posizione iniziale e la velocità iniziale sono nulle (\(s_0 = 0\) e \(v_0 = 0\)) la formula della velocità diventa: $$ v = at $$
Esempio pratico
Immagina di tenere una palla a una certa altezza.
Inizialmente la velocità della palla è nulla perché non si muove.
$$ v_0 = 0 $$
Se lasci cadere la palla l'accelerazione è quella di gravità (g ≈ 9.8 m/s²) che attira ogni corpo verso il centro della Terra.
Dopo un secondo (t = 1) la velocità di caduta della palla sarà:
\[ v = 9.8 \, \text{m/s}^2 \cdot 1 \, \text{s} = 9.8 \, \text{m/s} \]
Dopo due secondi (t = 2) la velocità di caduta della palla sarà:
\[ v = 9.8 \, \text{m/s}^2 \cdot 2 \, \text{s} = 19.6 \, \text{m/s} \]
Dopo 3 secondi (t = 3) la velocità di caduta della palla sarà:
\[ v = 9.8 \, \text{m/s}^2 \cdot 3 \, \text{s} = 29.4 \, \text{m/s} \]
La posizione della palla dopo tre secondi sarà:
\[ s = \frac{1}{2} \cdot 9.8 \, \text{m/s}^2 \cdot (3 \, \text{s})^2 = \frac{1}{2} \cdot 9.8 \cdot 9 = 44.1 \, \text{m} \]
Quindi, dopo soli 3 secondi, la palla avrà raggiunto una velocità di 29.4 m/s e sarà caduta di 44.1 metri.
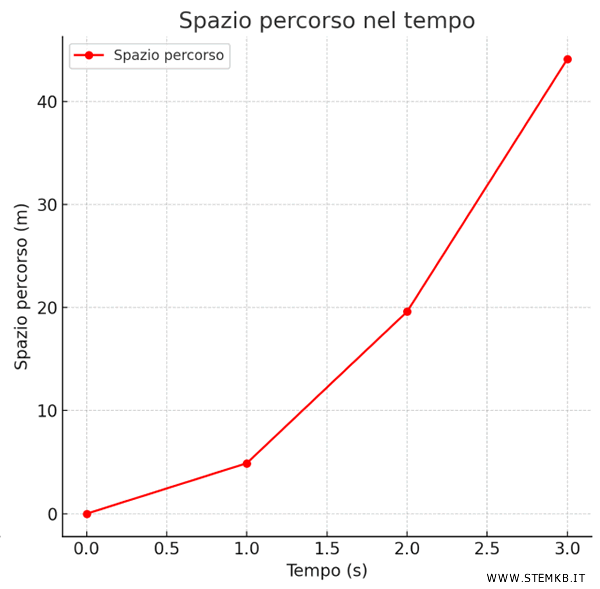
Ecco una tabella che mostra la velocità e lo spazio percorso dalla palla a diversi istanti di tempo, con l'accelerazione dovuta alla gravità \( g \approx 9.8 \, \text{m/s}^2 \):
\[
\begin{array}{|c|c|c|}
\hline
\text{Tempo } (t) \text{ [s]} & \text{Velocità } (v) \text{ [m/s]} & \text{Spazio percorso } (s) \text{ [m]} \\
\hline
0 & 0 & 0 \\
\hline
1 & 9.8 & 4.9 \\
\hline
2 & 19.6 & 19.6 \\
\hline
3 & 29.4 & 44.1 \\
\hline
\end{array}
\]
A partire da questi dati possiamo costruire il grafico dello spazio-tempo.
Come puoi vedere la velocità di caduta della palla aumenta con il tempo.
Nota che in assenza di resistenza dell'aria, tutti i corpi cadono con la stessa accelerazione indipendentemente dalla loro massa.
Questa accelerazione è dovuta alla forza di gravità e ha un valore approssimativo di \( g \approx 9.8 \, \text{m/s}^2 \).
Secondo la legge della caduta dei gravi di Galileo Galilei, in un vuoto (dove non c'è resistenza dell'aria), tutti gli oggetti cadono con la stessa accelerazione gravitazionale.
Questo significa che una piuma e una palla di cannone, lasciate cadere nello stesso momento e da la stessa altezza, raggiungeranno il suolo contemporaneamente.
Un esperimento famoso per dimostrare questo principio fu eseguito dall'astronauta David Scott sulla Luna durante la missione Apollo 15. Egli lasciò cadere contemporaneamente un martello e una piuma. Poiché la Luna non ha atmosfera, quindi non c'è resistenza dell'aria, entrambi gli oggetti caddero con la stessa accelerazione e toccarono il suolo lunare nello stesso momento. Questo esperimento dimostrò che, in assenza di resistenza dell'aria, la massa non influisce sulla velocità di caduta di un oggetto.

