Il gradiente di una funzione

Che cos'è il gradiente?

Il gradiente è un operatore vettoriale che misura come varia una quantità fisica nello spazio.

In termini più semplici, quando applichiamo il gradiente a una funzione scalare, una funzione che associa a ogni punto un singolo numero, otteniamo un vettore che punta nella direzione di massima crescita della funzione e ha una lunghezza proporzionale alla velocità di questa crescita.

Formalmente, se abbiamo una funzione scalare \( f(x, y, z) \) che dipende dalle coordinate spaziali \( x \), \( y \) e \( z \), il gradiente si calcola così:

\[ \nabla f = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} + \frac{\partial f}{\partial z} \vec{k} \]

Dove:

• \( \frac{\partial f}{\partial x} \), \( \frac{\partial f}{\partial y} \) e \( \frac{\partial f}{\partial z} \) sono le derivate parziali di \( f \) rispetto a ciascuna variabile;
• \( \vec{i} \), \( \vec{j} \), \( \vec{k} \) sono i versori delle direzioni \( x \), \( y \) e \( z \).

Se la funzione dipende solo da \( x \) e \( y \), il termine lungo \( z \) naturalmente scompare.

L'interpretazione fisica: come leggere il gradiente

Dal punto di vista intuitivo, il gradiente ci dice dove andare per trovare l'aumento massimo della funzione e quanto rapidamente la funzione cresce.

Come ha scritto Richard Feynman, famoso fisico e divulgatore, "la natura usa sempre la via più semplice", e il gradiente è proprio lo strumento che svela questa via nei campi di forze, nelle temperature, nelle altitudini e molto altro.

Se applichi il gradiente in un punto dello spazio ottieni due informazioni molto importanti:

• La direzione del gradiente è quella della massima crescita.
• Il modulo del gradiente misura la "ripidità" della salita.

Ad esempio, immagina di trovarti su una collina e di voler sapere in quale direzione devi camminare per salire più rapidamente.

Per saperlo ti basta trovare il gradiente della funzione nel punto in cui ti trovi.

Un esempio pratico: il gradiente di un paraboloide

Consideriamo la funzione:

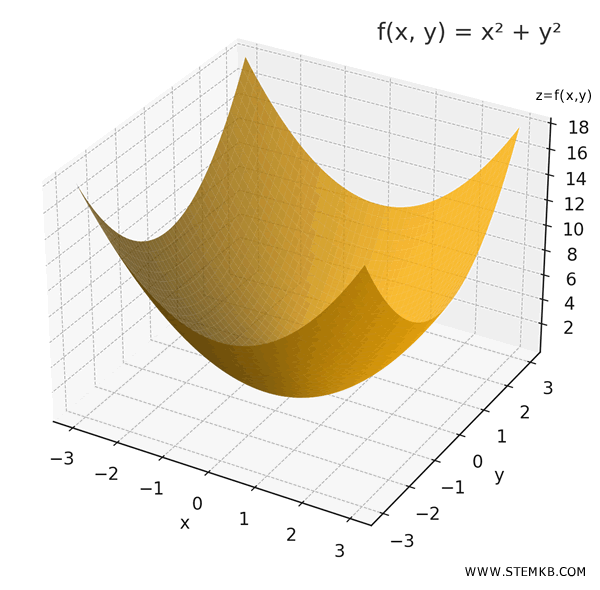
\[ f(x, y) = x^2 + y^2 \]

Questa funzione descrive un paraboloide, una superficie che cresce allontanandosi dall'origine.

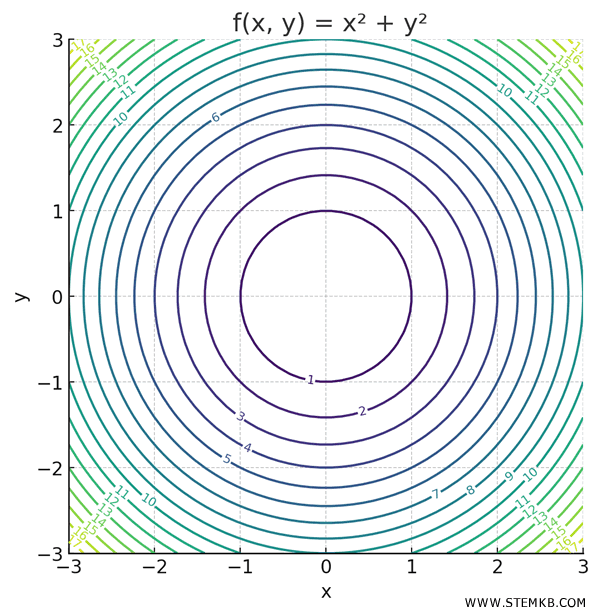
Per studiare meglio la funzione rappresentiamo anche le linee di livello.

Calcoliamo il gradiente:

1. Deriviamo rispetto a \( x \): \[  \frac{\partial f}{\partial x} = 2x \]
2. Deriviamo rispetto a \( y \): \[ \frac{\partial f}{\partial y} = 2y \]

Quindi il gradiente è:

\[ \nabla f = 2x \vec{i} + 2y \vec{j} \]

I versori sono i vettori unitari che rappresentano gli assi cartesiani x e y ossia $ \vec{i} = \binom 1 0  $ e $ \vec{j} = \binom 0 1 $

\[ \nabla f = 2x \cdot  \binom 1 0  + 2y \cdot \binom 0 1 \]

\[ \nabla f = \binom {2x} {2y} \]

Spesso per semplicità si indica anche in questo modo

\[ \nabla f = (2x, 2y) \]

Questa funzione cresce man mano che ci si allontana dall'origine.

In questo caso, in ogni punto \((x, y)\) il gradiente punta direttamente verso l'esterno rispetto all'origine: più ci si allontana, più il "ripido" aumenta.

Ad esempio, nel punto \((1,1)\), il gradiente è:

\[ \nabla f(1,1) = (2x, 2y) = (2,2) \]

Cioè un vettore che parte dal punto (1,1) e punta a \( 45^\circ \) rispetto agli assi verso il punto (1,1)+(2,2) = (3,3), lungo la bisettrice del primo quadrante.

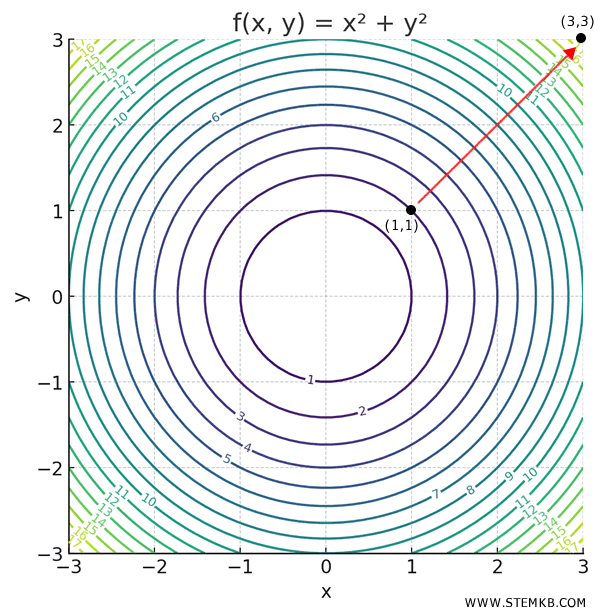
Con quale velocità avviene lo spostamento?

La velocità con cui f cambia quando ci muoviamo nella direzione di massima salita (cioè lungo il gradiente stesso) è proprio il modulo del gradiente:

\[ \|\nabla f(1,1)\| \;=\; \sqrt{(2x)^2 + (2y)^2} \]

\[ \|\nabla f(1,1)\| \;=\; \sqrt{(2 \cdot 1)^2 + (2 \cdot 1)^2} \]

\[ \|\nabla f(1,1)\| \;=\; \sqrt{4 + 4} = \sqrt{8} = 2.83 \]

Se percorriamo un piccolo spostamento unitario nella direzione di \(\nabla f\), il valore di \(f\) cresce di \(\|\nabla f\| = 2.83 \).

E' la massima crescita possibile della funzione a partire dal punto \( 1,1 \).

Ovviamente, il discorso cambia a seconda della funzione. Ad esempio, un'altra funzione potrebbe avere il gradiente che punta verso l'origine. Una cosa però non cambia mai... il gradiente punta sempre nella direzione di massima crescita della funzione. In un certo senso il gradiente è una vera e propria bussola che guida il comportamento delle funzioni scalari nello spazio.

La derivata direzionale

Spesso siamo interessati a sapere come varia una funzione non nella direzione massima, ma lungo una direzione specifica, per esempio lungo una strada o un sentiero.

Questo si calcola tramite la derivata direzionale, definita come:

\[ D_{\vec{v}} f = \nabla f \cdot \vec{v} \]

Dove \( \vec{v} \) è un vettore unitario che indica la direzione desiderata. Si tratta di un semplice prodotto scalare: una misura di quanto il gradiente "spinge" lungo \( \vec{v} \).

Un esempio pratico

Ad esempio, considera la funzione di prima:

\[ f(x, y) = x^2 + y^2 \]

Supponiamo di voler calcolare la derivata direzionale di \( f \) nel punto \( (1,1) \) lungo la direzione del vettore \( \vec{v} = (1,2) \) ossia verso il punto \( (1,1)+(1,2)=(1+1,1+2)=(2,3) \).

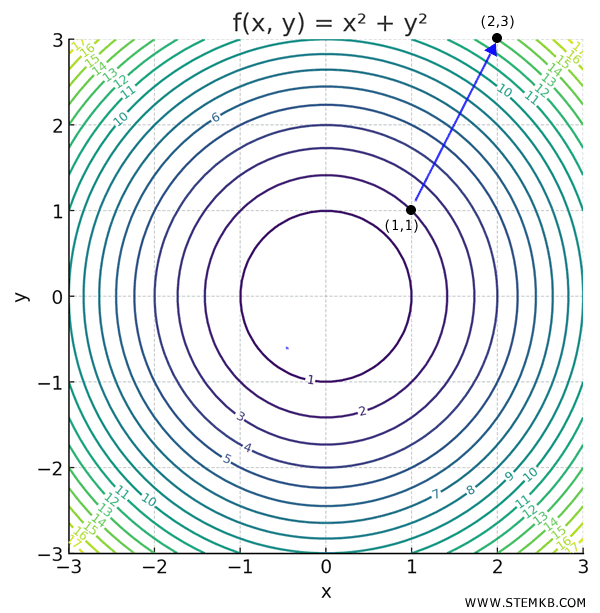
Per calcolare la derivata direzionale, \( \vec{v} \) dobbiamo prima normalizzare il vettore direzione, ossia dobbiamo trasformarlo in un vettore unitario (cioè di lunghezza 1).

Per prima cosa calcoliamo la sua norma (modulo):

\[ \|\vec{v}\| = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}  \]

Quindi il vettore unitario nella direzione di \( \vec{v} \) è:

\[ \vec{u} = \frac{ \vec{v} }{  \|\vec{v}\| } = \frac{(1,2)}{ \sqrt{5}} = \left(\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}}\right) \]

Abbiamo già visto prima che il gradiente della funzione è:

\[ \nabla f(x, y) = (2x, 2y) \]

Sostituiamo $ x=1 $ e $ y=1 $ nel gradiente è otteniamo la direzione di massima crescita nel punto \( (1,1) \).

\[ \nabla f(1,1) = (2 \times 1, 2 \times 1) = (2, 2) \]

Il gradiente nel punto \( (1,1) \) punta nella direzione \( (2,2) \) ossia verso il punto \( (1,1) + (2,2) = (1+2,1+2) = (3,3) \).

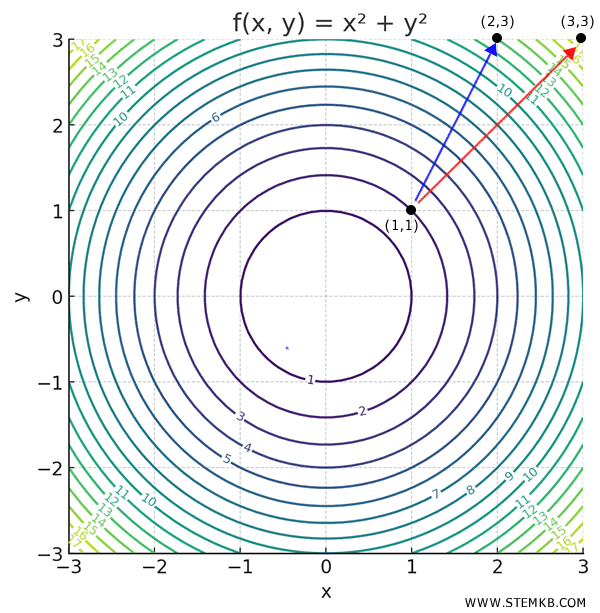
A questo punto possiamo calcolare la derivata direzionale tramite il prodotto scalare tra il gradiente $ \nabla f(1,1) = (2, 2)  $ e il vettore unitario della direzione $ \vec{u} =  \left(\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}}\right) $.

\[ D_{\vec{u}} f(1,1) = \nabla f(1,1) \cdot \vec{u}  \]

\[ D_{\vec{u}} f(1,1) = (2,2) \cdot \left(\frac{1}{ \sqrt{5}}, \frac{2}{\sqrt{5}}\right) \]

Facciamo il prodotto scalare:

\[ D_{\vec{u}} f(1,1) = 2 \times \frac{1}{\sqrt{5}} + 2 \times \frac{2}{\sqrt{5}} \]

\[ D_{\vec{u}} f(1,1) = \frac{2}{\sqrt{5}} + \frac{4}{\sqrt{5}}  = \frac{6}{\sqrt{5}} = 2.68 \]

La derivata direzionale di \( f \) nel punto \( (1,1) \) lungo la direzione \( (1,2) \) è 2.68.

Questo significa che, spostandoci dal punto \( (1,1) \) nella direzione di \( (1,2) \), la funzione \( f \) aumenta al tasso di 2.68 per unità di distanza percorsa. In altre parole, ogni passo lungo quella direzione fa crescere \( f \) di circa 2.68.

Come puoi notare, il tasso di crescita 2.68 nella direzione \(1,2 \) è inferiore al tasso di crescita del gradiente, circa 2.83 , che avevamo calcolato a partire dallo stesso punto (1,1). Questo accade perché il gradiente indica sempre la direzione di massima crescita della funzione.