Gli integrali
Nel calcolo infinitesimale esistono due tipi principali di integrali: l'integrale definito e l'integrale indefinito.
L'integrale indefinito
L'integrale indefinito è l'operazione inversa della derivazione. $$ \int f(x) \ dx $$
Se hai una funzione f(x), l'integrale indefinito della funzione, indicato con ∫f(x)dx, è una famiglia di funzioni primitive F(x) che, una volta derivate, sono uguali a f(x).
$$ \int f(x) \ dx = F(x) + C $$
Dove dx indica la variabile di integrazione, in questo caso la x, e C è una costante di integrazione.
La derivata della funzione primitiva F(x)+C è uguale alla funzione "integranda" f(x).
$$ \frac{d \ F(x)+C}{dx} = f(x) $$
Nota che il risultato non è una funzione ma una famiglia di infinite funzioni, perché la derivata della costante è uguale a zero qualunque sia il valore della costante.
Ecco un esempio pratico.
Considera l'integrale di f(x)=2x
$$ \int 2x \ dx $$
Il risultato dell'integrale è la famiglia di funzioni F(x)=x2+C
$$ \int 2x \ dx = x^2 + C $$
Questo perché una volta derivata, qualsiasi funzione del tipo F(x)=x2+C è uguale alla funzione integranda f(x)=2x
$$ \frac{d \ x^2+C}{dx} = 2x $$
Dove C è una costante a cui puoi assegnare un valore qualsiasi.
La costante non è importante, in quanto la derivata di una costante è uguale a zero.
Ad esempio, la derivata di x2+1 e di x2+2 è comunque 2x
$$ \frac{d \ x^2+1}{dx} = 2x $$
$$ \frac{d \ x^2+2}{dx} = 2x $$
$$ \vdots $$
Come si trova la funzione primitiva? Per risolvere un integrale indefinito puoi usare varie tecniche: l'integrazione per sostituzione, l'integrazione per parti, l'integrazione delle funzioni razionali mediante la divisione fra polinomi o la decomposizione in fratti semplici ecc.
L'integrale definito
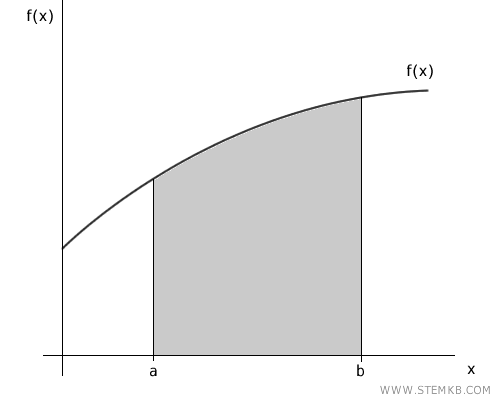
L'integrale definito di una funzione è un numero, che puoi immaginare come l'area sotto il grafico della funzione in un intervallo specifico (a,b). $$ \int_a^b f(x) \ dx $$
Ricorda che l'integrale definito non è una funzione ma un numero.
In questo caso, per scrivere l'integrale devi indicare anche gli estremi dell'intervallo di integrazione (a,b).
Ad esempio, l'integrale definito della funzione f(x) dall'estremo inferiore "a" all'estremo superiore "b"
$$ \int_a^b f(x) \ dx $$
Il risultato è un numero che rappresenta l'area tra la curva f(x) e l'asse x nell'intervallo (a,b).
Ad esempio, considera l'integrale della funzione 2x nell'intervallo a=1 e b=3
$$ \int_1^3 2x \ dx $$
Per risolvere questo integrale devi prima trovare la funzione primitiva F(x), risolvendo l'integrale indefinito
$$ F(x) = \int 2x \ dx = x^2 + C $$
Non considerare la costante C
$$ F(x) = x^2 $$
Una volta trovata la funzione primitiva F(x), devi applicare il teorema fondamentale del calcolo integrale che collega le due forme di integrale e fornisce un modo per calcolare gli integrali definiti.
$$ \int_a^b f(x) \ dx = F(b) - F(a) $$
In questo caso gli estremi sono a=1 e b=3
$$ \int_3^5 2x \ dx = F(3) - F(1) $$
Sai già che la funzione primitiva è F(x)=x2
Quindi, F(1)=12 e F(3)=32
$$ \int_3^5 2x \ dx = 3^2 - 1^2 $$
$$ \int_3^5 2x \ dx = 9 - 1 $$
$$ \int_3^5 2x \ dx = 8 $$
Quindi, l'area tra il grafico della funzione f(x)=2x nell'intervallo (1,3) è uguale a 8.
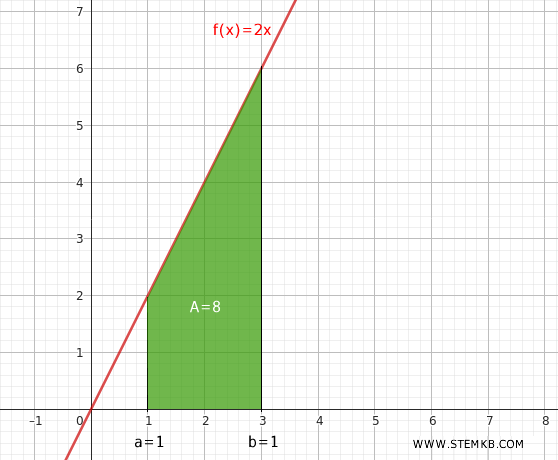
In questo esempio il grafico della funzione è un grafico lineare ed elementare. L'area è composta da un quadrato e un triangolo rettangolo.
Puoi verificare tu stesso che, nell'intervallo (1,3), l'area sotto il grafico è effettivamente uguale a 8.

