
La funzione cotangente
In trigonometria la cotangente di un angolo θ è definita come il rapporto tra il cateto adiacente all'angolo e il cateto opposto. Si indica con il simbolo cot() oppure cotg() $$ \cot(θ) = \frac{ \text{cateto adiacente} }{ \text{cateto opposto} } $$
La cotangente può variare su tutto l'insieme dei numeri reali e il suo ciclo si ripete ogni 180 gradi.
Per esempio, se abbiamo un triangolo rettangolo con un angolo di 45 gradi, e il lato adiacente a questo angolo è lungo 10 cm, mentre il lato opposto misura 10 cm, la cotangente di questo angolo sarà:
$$ \cot(45°) = \frac{ 10 }{ 10 } = 1 $$
Il valore della cotangente di un angolo può essere qualsiasi numero reale, a seconda della posizione dell'angolo nel triangolo.
Vediamo un esempio pratico.
Disegna un cerchio con centro O e un raggio OA di lunghezza 1 (raggio unitario).
Scegli un punto P sulla circonferenza.
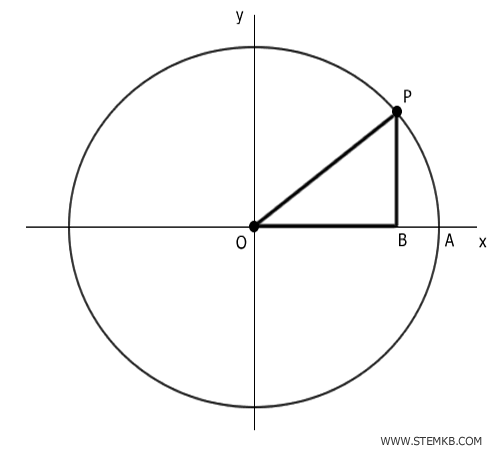
Disegna un triangolo rettangolo con l'ipotenusa che collega il centro della circonferenza O con il punto P.
Considera l'angolo θ
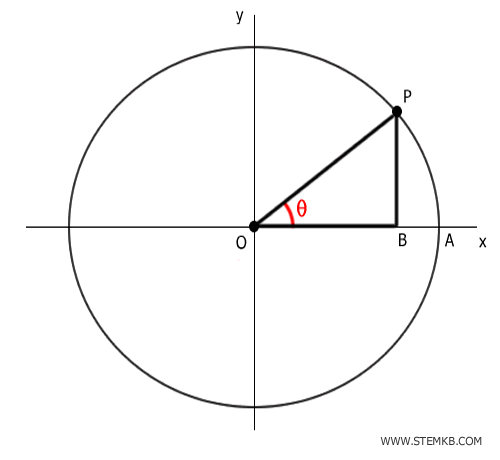
La cotangente è il rapporto tra il cateto adiacente all'angolo (OB) e il cateto opposto (BP)
$$ \cot(θ) = \frac{\overline{OB}}{ \overline{BP} } $$
Considerando che OB è il coseno e BP è il seno dell'angolo, puoi scrivere la cotangente anche come il rapporto tra il coseno e il seno
$$ \cot(θ) = \frac{\cos θ}{ \sin θ} $$
Nota. Sai già che la tangente è il rapporto tra il seno e il coseno. $$ \tan(θ) = \frac{\sin θ}{ \cos θ} $$ Quindi, puoi scrivere la cotangente anche come il reciproco della tangente $$ \cot(θ) = \frac{1}{ \tan θ} = \frac{1 }{\frac{\sin θ}{ \cos θ}} = \frac{\cos θ}{ \sin θ} $$
Dal punto di vista geometrico la cotangente è uguale alla lungheza del segmento OC.

Se l'angolo è compreso tra 0 e 90 gradi, la cotangente è positiva, mentre se l'angolo è compreso tra 90 e 180 gradi, la cotangente diventa negativa.
La cotangente è nulla se l'angolo è uguale a 90° mentre è indefinita se l'angolo è uguale a 0 o 180°.
Come la tangente anche la cotangente è una funzione periodica, il che significa che ripete il suo ciclo adintervalli regolari.
In particolare, il periodo della cotangente è di 180 gradi (o π radianti), il che significa che il valore della cotangente di un angolo è lo stesso di quello di un angolo di 180 gradi in più o in meno.
Per esempio, la cotangente di un angolo di 30 gradi è la stessa di quella di un angolo di 210 gradi, dato che 210 = 30 + 180.
La cotangente di un angolo θ è una misura adimensionale. Rimane invariata indipendentemente dalla dimensione della circonferenza, poiché si ottiene dal rapporto di due lunghezze.

