Come trovare il coniugato di un numero complesso su Octave

In questa lezione ti spiego come si trova il coniugato di un numero complesso su Octave.

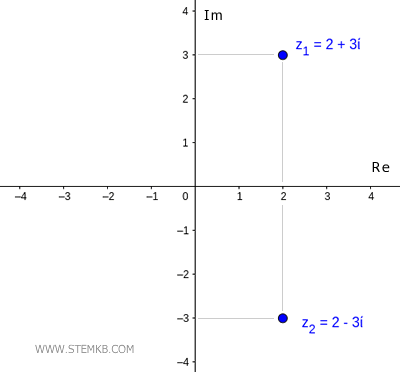
Cos'è il coniugato di un numero complesso? Il coniugato di un numero complesso z=a+bi è un numero complesso che ha la stessa parte reale e la parte immaginaria cambiata di segno. Ad esempio, il numero complesso z₁=2+3i ha come coniugato il numero complesso z₂=2-3i, e viceversa.

Ti faccio un esempio pratico.

Definisci su Octave il numero complesso z=2+3i tramite la funzione complex(2,3)

>> z=complex(2,3)
ans = 2 + 3i

Per ottenere il coniugato di z usa la funzione conj()

>> conj(z)
ans = 2 - 3i

Il risultato è il numero coniugato z=2-3i.

A cosa serve calcolare il coniugato?

L'uso del coniugato semplifica alcune operazioni di calcolo con i numeri complessi.

Ad esempio, il prodotto di un numero complesso per il suo coniugato è uguale al quadrato del suo modulo.

Moltiplica il numero complesso z per il suo coniugato conj(z). Il prodotto è uguale a 13.

>> z*conj(z)
ans = 13

Ora calcola il modulo del numero complesso z tramite la funzione abs()

Il modulo del numero complesso è circa 3.6

>> abs(z)
ans = 3.6056

Infine calcola il quadrato del modulo di z

Il risultato è sempre 13.

>> (abs(z))^2
ans = 13.000

Questo vuol dire che per trovare il modulo di un numero complesso puoi anche calcolare la radice quadrata del prodotto del numero complesso per il suo coniugato.

>> sqrt(z*conj(z))
ans = 3.6056

Se questa lezione di StemKB sull'utilizzo dei numeri complessi su Octave ti piace, continua a seguirci.