Come trovare l'angolo e il modulo di un numero complesso su Octave

In questa lezione ti spiego come si calcola l'angolo (argomento) e il modulo di un numero complesso su Octave.

Cos'è il modulo e l'angolo di un numero complesso? Ogni numero complesso z=a+bi puoi rappresentarlo sul piano complesso alle coordinate (a,b).

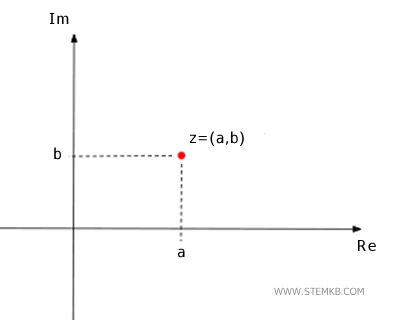
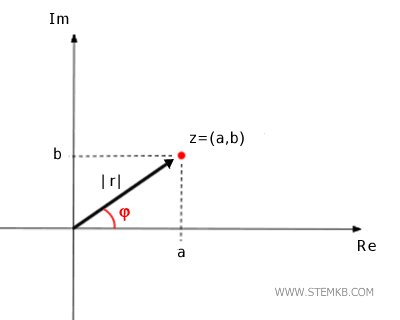
Quindi, ogni punto del piano è un numero complesso diverso ed è univocamente raggiungibile dall'origine tramite un vettore. La lunghezza r=|z| del vettore è detta modulo del numero complesso z. L'angolo φ del vettore misurato in senso antiorario rispetto al semiasse positivo (Re) è detto argomento del numero complesso.

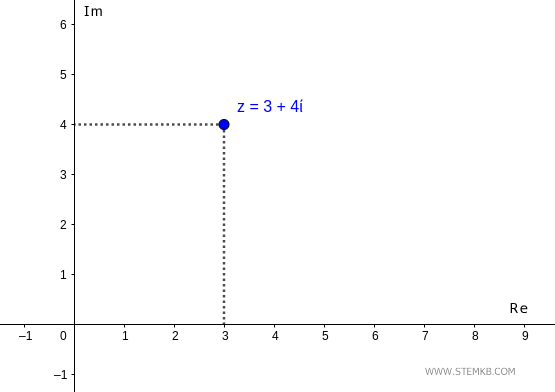
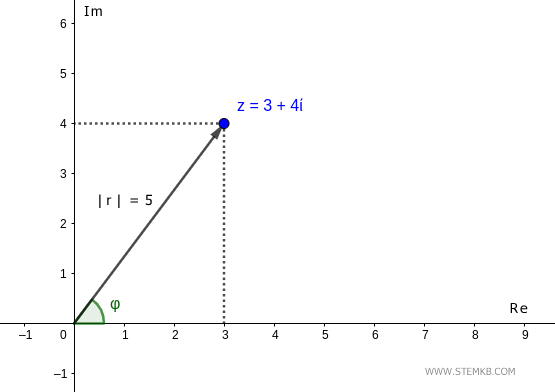
Ad esempio, considera il numero complesso z=3+4i

Sul piano complesso il numero z si trova in punto alle coordinate (3,4).

Questo punto è raggiungibile dall'origine da un solo vettore di lunghezza r e angolo φ.

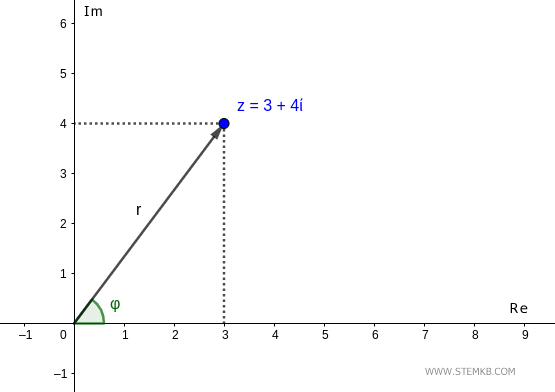
Per calcolare il modulo r=|z| del numero complesso, ossia la lunghezza del vettore, usa la funzione abs() di Octave

>> abs(z)
ans= 5

Quindi, il modulo del numero complesso z=3+4i è uguale a 5

Detto in altri termini, il vettore che collega l'origine con il punto (3,4) ha una lunghezza pari a cinque.

Per calcolare l'angolo (argomento) del numero complesso, invece, usa la funzione angle()

>> angle(z)
ans = 0.92730

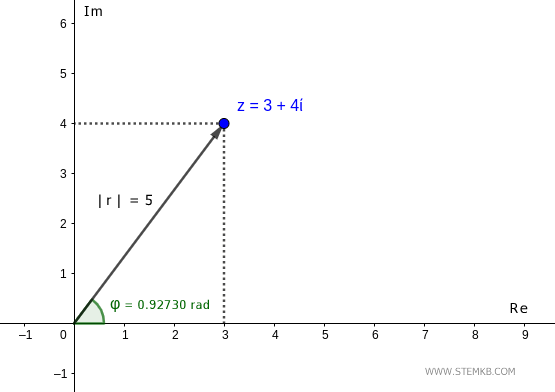
Octave restituisce l'angolo in radianti.

In questo caso l'argomento del numero complesso z=3+4i è 0.92730 radianti. Circa 53°.

Se questa lezione di StemKB su Octave è utile, continua a seguirci.