
Come fare i numeri complessi su Scilab
In questa lezione ti spiego come si scrivono i numeri complessi su Scilab tramite un esempio pratico.
Vai su Scilab e digita z1=complex(3,4) per scrivere il numero complesso 3+4i
Poi dai invio
z1=complex(3,4)
In alternativa, puoi definire il numero complesso 3+4i anche usando questa sintassi. Il risultato finale è lo stesso.
z1 = 3 + 4 * %i
Dove %i è la costante usata da Scilab per indicare l'unità immagnaria.
Ora digita z2=complex(2,3) per scrivere il numero complesso 2+3i
Poi dai invio
z1=complex(2,3)
Hai appena creato due variabili complesse.
Le puoi usare per compiere qualsiasi operazione matematica.
Ad esempio, puoi calcolare la somma dei numeri complessi
z1+z2
ans =
5.+7.i
Scilab calcola l'operazione tra i due numeri complessi e visualizza il risultato.
Per accedere alla parte reale del numero complesso, utilizza la funzione real()
Ad esempio, nella variabile z1 è assegnato il numero complesso 2+3i
Digita real(z1) sulla riga comandi.
real(z1)
La funzione real() ti restituisce il coefficiente della parte reale del numero complesso, ossia 2.
2
Allo stesso modo puoi accedere alla parte immaginaria del numero complesso, usando la funzione imag().
Ad esempio, digita imag(z1) sulla riga di comando.
imag(z1)
La funzione imag() visualizza il coefficiente della parte immaginaria del numero complesso 2+3i ossia 3
3
Ricorda che un numero complesso z=x+yi è anche un punto (x;y) del piano di Gauss e può essere rappresentato tramite un vettore che congiunge l'origine con il punto (x;y)
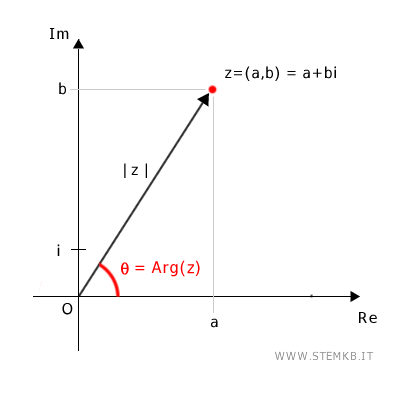
La lunghezza |z| del vettore è detta modulo (o valore assoluto) mentre l'angolo θ del vettore rispetto al semiasse positivo delle x è detto argomento del numero complesso.
Conoscere la parte reale e immaginaria del numero complesso z=x+yi ti permette di trovare l'angolo (argomento)
$$ θ = \tan^{-1} \frac{y}{x} $$
Traduci la formula precedente in un'espressione matematica su Scilab
atan(imag(z1)/real(z1))
Nel caso del numero complesso z1=3+4i l'angolo è circa 0,98 radianti.
0.9827937
Per conoscere anche il modulo, ossia la distanza tra l'origine e il numero complesso sul piano di Gauss, puoi usare la funzione del valore assoluto abs()
abs(z1)
Il modulo (magnitudine) del numero complesso z1=3+4i è circa 3,6
3.6055513
Se questa guida di StemKB ti piace, continua a seguirci.

