La matrice di adiacenza di un grafo
La matrice di adiacenza di un grafo è una tabella quadrata (matrice) utilizzata per rappresentare quali vertici nel grafo sono adiacenti, ossia direttamente connessi da uno spigolo.
E' uno strumento molto utile per rappresentare un grafo in forma matematica.
Come costruire la matrice di adiacenza di un grafo
Sappiamo che un grafo è composto da vertici (o nodi) e spigoli (o archi) che collegano questi vertici. Immagina i vertici come punti e gli spigoli come linee che collegano alcuni di questi punti.
Se il grafo ha \( n \) vertici, la matrice di adiacenza ha dimensione \( n \times n \), ovvero è una matrice quadrata formata da $ n $ righe e $ n $ colonne. .
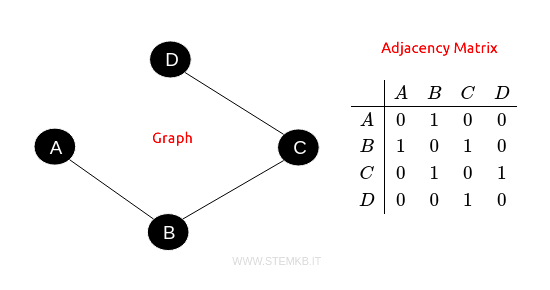
Ogni riga e ogni colonna della matrice è associata a un vertice del grafo.
Gli elementi della matrice possono essere 0 o 1:
- 1 significa che c'è uno spigolo diretto tra i vertici corrispondenti.
- 0 significa che non c'è uno spigolo diretto tra i vertici corrispondenti.
In alcuni casi, altri numeri se gli spigoli hanno pesi o se ci sono più spigoli tra lo stesso paio di vertici.
Esempio
Immagina un piccolo grafo con 4 vertici: \( A, B, C, \) e \( D \).
Supponiamo che ci siano spigoli tra \( A \) e \( B \), \( B \) e \( C \), e \( C \) e \( D \).
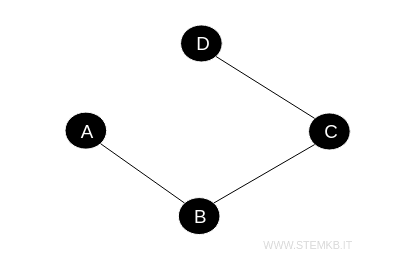
La matrice di adiacenza per questo grafo, con i vertici ordinati come \( A, B, C, D \), sarà:
$$
\begin{array}{c|cccc}
& A & B & C & D \\
\hline
A & 0 & 1 & 0 & 0 \\
B & 1 & 0 & 1 & 0 \\
C & 0 & 1 & 0 & 1 \\
D & 0 & 0 & 1 & 0 \\
\end{array}
$$
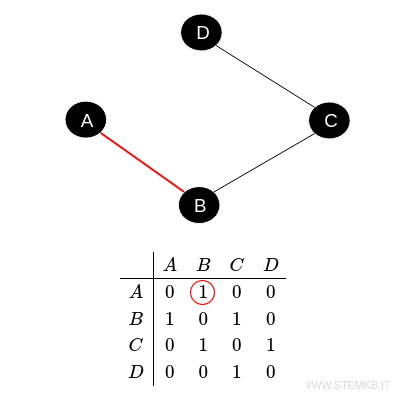
Le celle che non hanno collegamenti diretti tra di loro hanno un valore di 0 mentre quelle collegate hanno un valore uguale a 1.
Ad esempio, la cella nella riga \( A \) e colonna \( B \) ha un valore di 1 perché c'è un spigolo che collega \( A \) a \( B \).
La matrice di adiacenza è simmetrica per i grafi non direzionati, cioè se un vertice \( A \) è collegato a \( B \), anche \( B \) è collegato a \( A \).
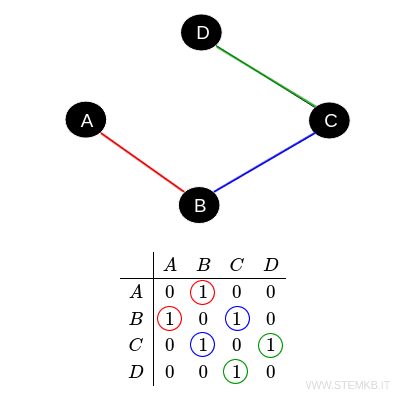
Inoltre, se il grafo ha cicli, cioè spigoli che partono e arrivano allo stesso vertice, sulla diagonale principale della matrice ci saranno valori diversi da zero.
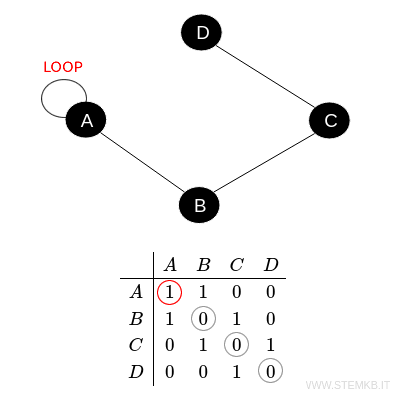
Questo strumento è particolarmente utile perché permette di visualizzare e analizzare rapidamente le relazioni tra i vertici in un grafo, e facilita l'implementazione di algoritmi sui grafi nei computer.
La matrice di adiacenza nei digrafi
Nei digrafi, o grafi direzionati, la matrice di adiacenza funziona in modo leggermente diverso rispetto ai grafi non direzionati.
Cos'è un digrafo? Un digrafo è un tipo di grafo in cui gli spigoli hanno una direzione, cioè partono da un vertice e arrivano a un altro.
La matrice di adiacenza di un digrafo continua a essere una matrice quadrata \( n \times n \) se il grafo ha \( n \) vertici.
In questo caso, però, le righe rappresentano i vertici di partenza e le colonne rappresentano i vertici di arrivo.
- 1 nella posizione \( (i, j) \) indica che esiste un arco che va dal vertice \( i \) al vertice \( j \).
- 0 nella posizione \( (i, j) \) indica che non esiste un arco diretto da \( i \) a \( j \).
Esempio
Consideriamo un digrafo con quattro vertici \( A, B, C, \) e \( D \) con gli archi direzionati da \( A \) a \( B \), da \( B \) a \( C \), e da \( C \) a \( D \).
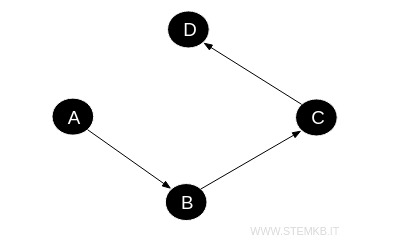
La matrice di adiacenza per questo digrafo sarà:
$$ \begin{array}{c|cccc}
& A & B & C & D \\
\hline
A & 0 & 1 & 0 & 0 \\
B & 0 & 0 & 1 & 0 \\
C & 0 & 0 & 0 & 1 \\
D & 0 & 0 & 0 & 0 \\
\end{array} $$
In questo caso, il valore "1" nella matrice indica la direzione dell'arco.
Per esempio, \( A \) ha un arco diretto verso \( B \), ma non il contrario.
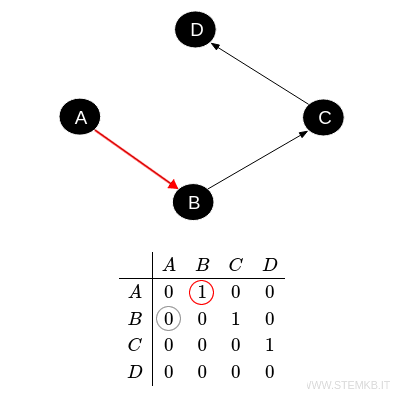
Questo significa che, come avrai già notato, la matrice di adiacenza di un digrafo non è simmetrica, a meno che il digrafo non abbia tutti gli archi che vanno in entrambe le direzioni tra gli stessi nodi.
La matrice di adiacenza in un digrafo può essere utilizzata anche per determinare se esistono percorsi da un vertice a un altro e per analizzare la struttura del grafo in termini di connettività e raggiungibilità. Utilizzando questa rappresentazione, è possibile eseguire algoritmi specifici per digrafi, come la ricerca di percorsi più brevi, il calcolo di componenti fortemente connessi, e altre analisi di rete che richiedono la direzionalità degli archi.

