
L'argomento del numero complesso
L'argomento di un numero complesso misura l'angolo che si crea tra l'asse reale positivo (Re) e il vettore che unisce l'origine al punto z=(a;b) associato al numero complesso z=a+bi sul piano di Gauss.
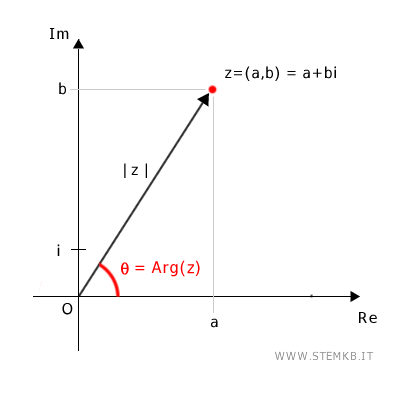
In genere l'argomento è indicato con Arg(z) $$ \theta = \text{Arg(z)} $$ Si misura in gradi oppure in radianti.
Immagina di avere un numero complesso, chiamiamolo z.
Questo numero puoi scriverlo in forma algebrica come z = a + bi, dove "a" è la parte reale e "bi" è la parte immaginaria.
$$ z = a+bi $$
Se rappresenti questo numero nel piano complesso, l'asse x misura il coefficiente "a" della parte reale mentre l'asse y misura il coefficiente "b" della parte immaginaria.
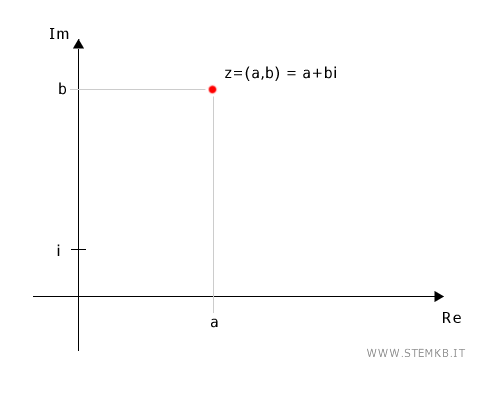
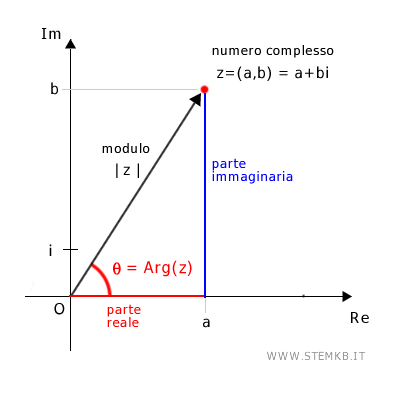
Ora, pensa a un vettore che parte dall'origine, il punto (0;0), e arriva al punto rappresentato dal tuo numero complesso, (a,b).
L'angolo tra l'asse Re positivo e il vettore è l'argomento del numero complesso z.
Ad esempio, il numero complesso z=4+3i corrisponde al punto (a;b)=(4;3) del piano di Gauss.
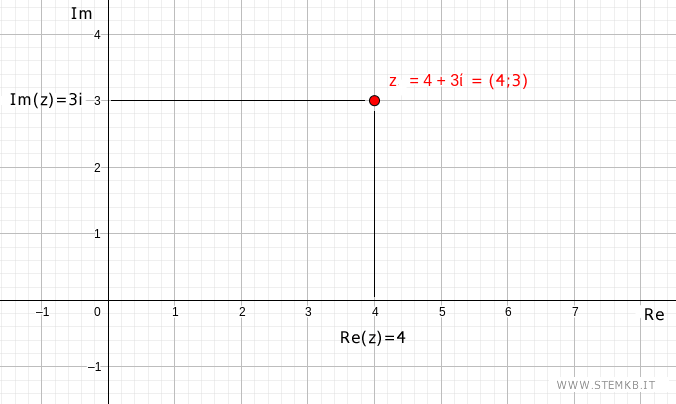
Traccia un vettore o un segmento che congiunge l'origine O con il punto (4;3),
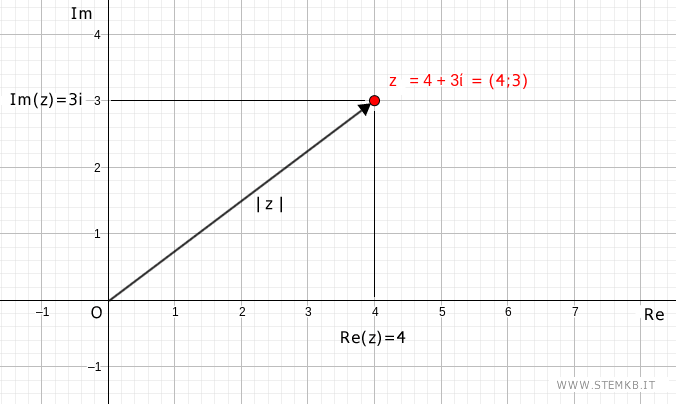
L'angolo che questo vettore forma con l'asse delle x positive è l'argomento del numero complesso z=4+3i.
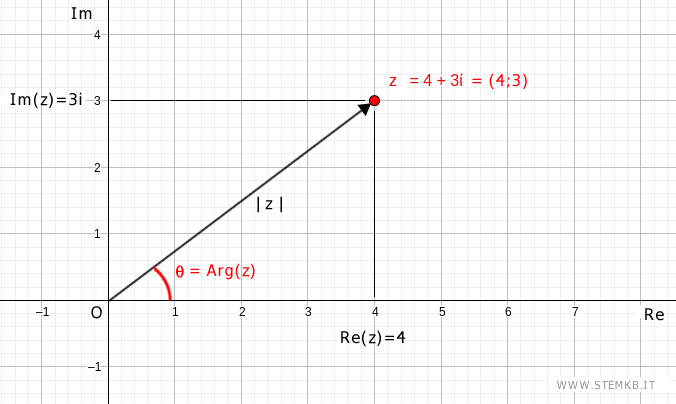
Come si calcola l'argomento del numero complesso?
Per ottenere l'argomento di un numero complesso puoi usare la funzione trigonometrica dell'arcotangente.
Calcola l'arcotangente del rapporto dei coefficienti b/a.
$$ \arg(z) = \arctan( \frac{b}{a} ) $$
Il risultato è l'argomento del numero complesso.
Ricorda che l'argomento è sempre un angolo. Quindi, puoi misurarlo indifferentemente sia in gradi che in radianti. C'è però un aspetto importante da ricordare: la funzione arcotangente può dare solo valori compresi tra -π/2 e π/2 (o -90 e 90 gradi). Quindi, se il coefficiente "a" è negativo, dovrai aggiustare l'angolo aggiungendo π radianti (o 180 gradi) al risultato.
In questo caso i coefficienti del numero complesso sono a=4 e b=3
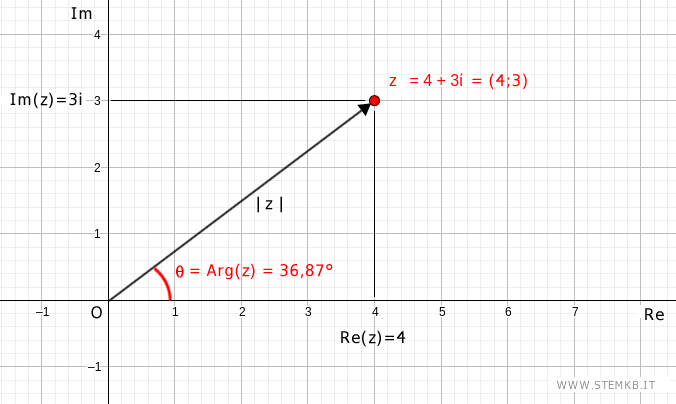
$$ \arg(z) = \arctan( \frac{3}{4} ) = 36.87° $$
Pertanto, l'argomento del numero complesso z=4+3i è uguale a 36,87° gradi.
Un ultimo punto da tenere a mente è che l'argomento di un numero complesso non è unico perché ,se aggiungi o sottrai multipli di 2π (o 360 gradi), otterrai altri argomenti validi per lo stesso numero complesso. Ad esempio, il numero complesso z=4+3i ha l'argomento θ=36,87°. E' altrettanto valido indicare come argomento qualsiasi altro angolo di ampiezza pari a $$ \theta = 36,87° + k \cdot 360° $$ Dove k è un numero intero qualsiasi.

