
La sottrazione tra due numeri complessi
In questa lezione ti spiego come fare la sottrazione tra due numeri complessi.
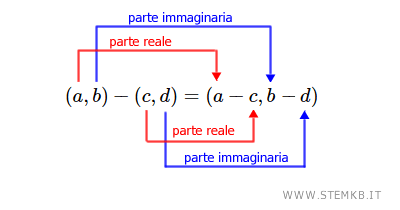
Per calcolare la differenza tra due numeri complessi (a,b) e (c,d) devi sottrarre i rispettivi elementi della coppia a-c e b-d $$ (a,b)-(c,d)=(a-c,b-d) $$
In pratica devi sottrarre tra loro la parte reale (rossa) e la parte immaginaria (blu) del primo numero complesso (minuendo) meno quella del secondo numero (sottraendo).
Ti faccio un esempio pratico
Prendi due numeri complessi qualsiasi
$$ z_1 = (2,3) = 2+3i $$
$$ z_2 = (4,2) = 4+2i $$
Ecco i due numeri sul piano complesso
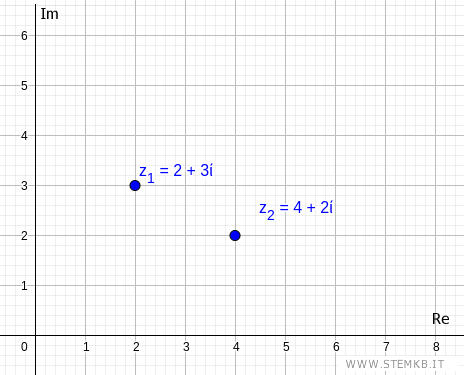
Sottrai la parte reale e la parte immaginaria del primo numero complesso (z1) meno quella del secondo numero (z2).
$$ z_1 - z_2 = (2,3) - (4,2) = (2-4,3-2) = (-2,1) $$
La differenza dei due numeri complessi è il numero complesso (-2,1) ossia -2+i
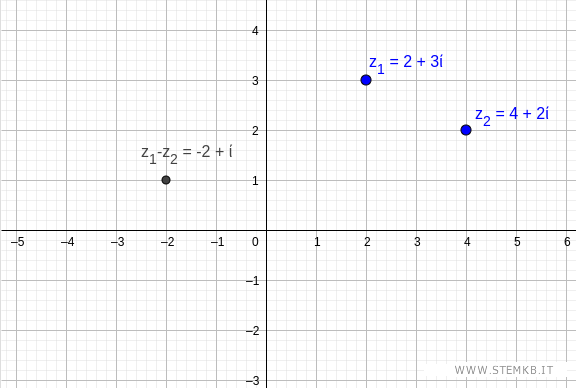
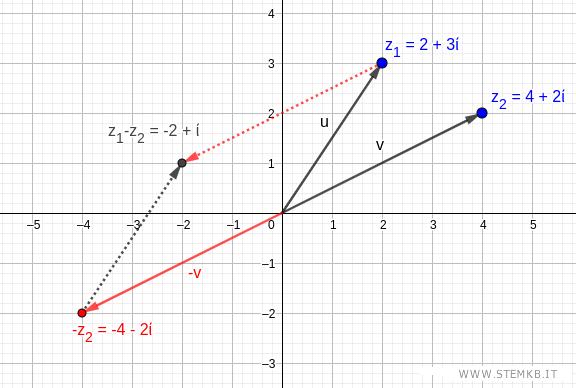
Dal punto di vista grafico la differenza tra due numeri complessi puoi calcolarla anche usando la somma vettoriale.
Trova il vettore opposto -v del secondo numero complesso (sottraendo)
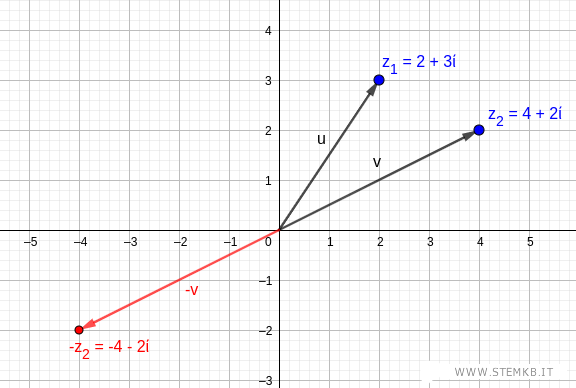
Poi somma il vettore u del primo numero complesso (minuendo) con il vettore opposto -v del secondo numero complesso (sottraendo) tramite il metodo del parallelogramma o il metodo punta-coda.
Il risultato finale è la differenza z1-z2 dei due numeri complessi.
Puoi fare la sottrazione dei numeri complessi anche quando sono in forma algebrica
$$ z_1-z_2 = (2,3i)-(4+2i) $$
Devi semplicemente associare e sottrarre tra loro la parte reale e la parte immaginaria dei due numeri complessi.
$$ z_1+z_2 = (2+3i)-(4+2i) = (2-4)+(3i-2i) = -2+i $$
Il risultato è lo stesso.
Se questa lezione di StemKB sui numeri complessi ti piace, continua a seguirci.

