
Il modulo di un numero complesso
Il modulo di un numero complesso è la distanza tra l'origine O e il punto rappresentato dal numero complesso z=(a;b) nel piano complesso.
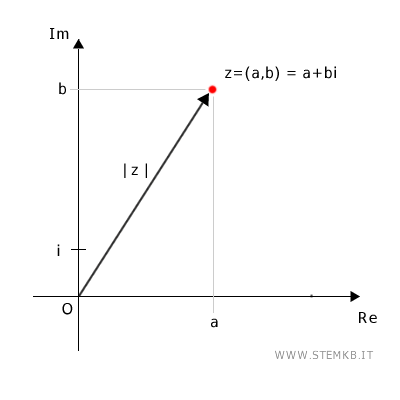
In genere il modulo di un numero complesso z si indica con il simbolo |z|.
Un numero complesso è rappresentato in forma algebrica come z = a + bi, dove a è la parte reale e b è la parte immaginaria.
$$ z = a+bi $$
Il modulo del numero complesso si calcola usando il teorema di Pitagora:
$$ |z| = \sqrt{ a^2 + b^2 } $$
In altre parole, il modulo |z| di un numero complesso z è l'ipotenusa del triangolo rettangolo formato dai segmenti che rappresentano la parte reale e la parte immaginaria di un numero complesso z nel piano complesso.
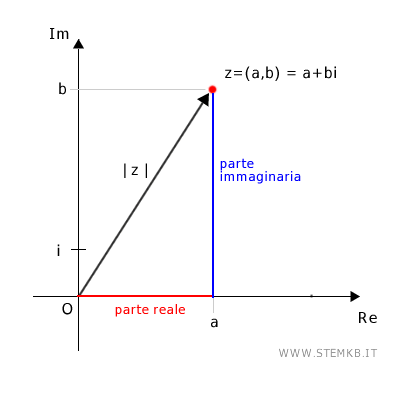
Ricorda che sul piano complesso (o piano di Gauss) il numero z=a+bi è rappresentato dal punto (a;b).
I coefficienti "a" e "b" della parte reale e immaginaria identificano le coordinate del punto.
A cosa serve il modulo di un numero complesso? Il modulo di un numero complesso è un concetto fondamentale nel campo dei numeri complessi. È uno strumento utile non solo per la comprensione teorica dei numeri complessi, ma anche per applicazioni pratiche in vari campi come l'ingegneria elettrica, l'informatica, la fisica e molti altri.
Se non ti è chiara questa spiegazione rapida, continua a leggere questa pagina.
Nel paragrafo seguente ti spiego in modo più semplice, passo dopo passo, cos'è il modulo di un numero complesso e come si calcola.
Una spiegazione più semplice e dettagliata passo dopo passo
I numeri complessi possono sembrare, come suggerisce il nome, complessi. Ma, una volta compresi, si rivelano uno strumento estremamente potente nel mondo della matematica, fisica e ingegneria.
Uno dei concetti fondamentali da capire quando si lavora con i numeri complessi è il modulo del numero complesso.
Prima di tutto, cos'è un numero complesso?
Un numero complesso è un numero che puoi rapresentare nella forma a + bi, dove a e b sono numeri reali e i è l'unità immaginaria, che ha la proprietà i2 = -1.
$$ z = a + bi $$
Dove "a" è la parte reale del numero complesso e "bi" è la parte immaginaria.
$$ Re(z) = a $$
$$ Im(z) = bi $$
Ad esempio, considera il numero complesso z=4+3i
$$ z = 4 + 3i $$
La parte reale del numero complesso è Re(z)= 4 e la parte immaginaria è Im(z) = 3i
$$ Re(z) = 4 $$
$$ Im(z) = 3i $$
Quindi, i coefficienti del numero complesso della parte reale e immaginaria del numero sono a=4 e b=3.
Puoi rappresentare i numeri complessi su un piano bidimensionale chiamato piano complesso o piano di Argand-Gauss.
Ad esempio, il numero complesso z=4+3i è rappresentato dal punto (4;3) sul piano complesso.
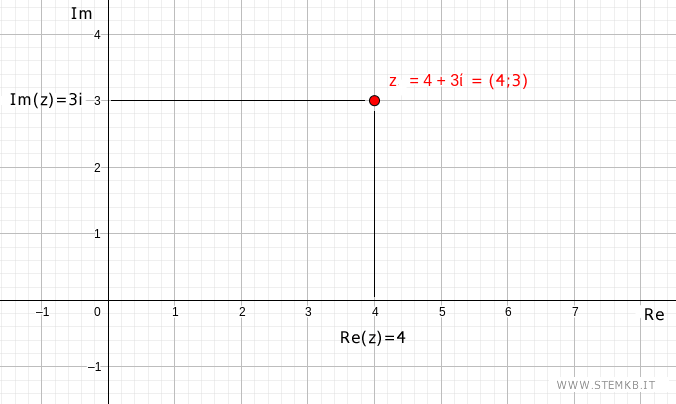
Un generico numero complesso a + bi può essere visualizzato come un punto (a;b) nel piano di Gauss, dove l'asse orizzontale rappresenta la parte reale, mentre l'asse verticale rappresenta la parte immaginaria. Ogni punto del piano di Gauss è un numero complesso e viceversa, ogni numero complesso è un punto del piano di Gauss.
Il modulo di un numero complesso, denotato come |z| se il nostro numero complesso è z, è la distanza tra l'origine O e il punto (4;3)
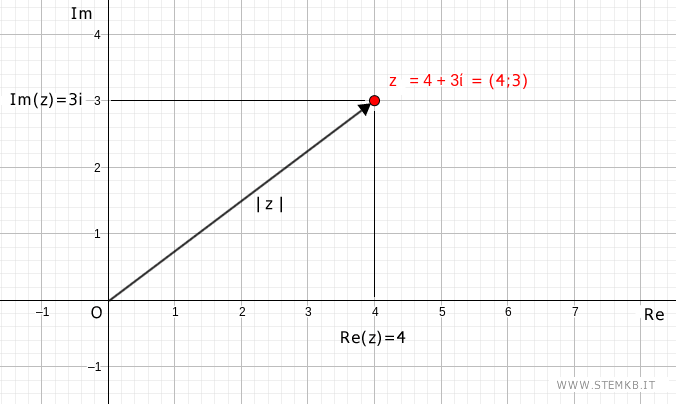
In altre parole, è la lunghezza del vettore che parte dall'origine e termina nel punto (a;b)=(4;3) del piano complesso, dove "a" è il coefficiente della parte reale del numero complesso e "b" è il coefficiente della parte immaginaria.
Come puoi notare, il punto e l'origine formano un triangolo rettangolo.
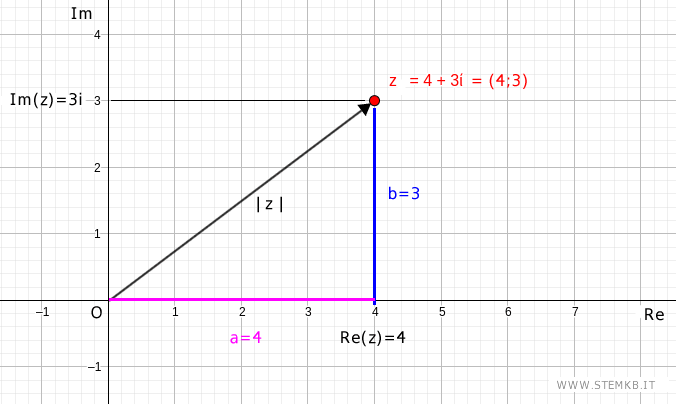
L'ipotenusa del triangolo rettangolo coincide con il modulo del numero complesso |z|.
Quindi, per calcolare il modulo di un numero complesso z = a + bi puoi utilizzare la formula del teorema di Pitagora.
$$ |z| = \sqrt{ a^2 + b^2 } $$
Questo spiega perché utilizziamo il Teorema di Pitagora per calcolare il modulo di un numero complesso.
In questo caso i coefficienti della parte reale e immaginaria del numero complesso z sono a=4 e b=3
Quindi, il modulo del numero complesso è 5.
$$ |z| = \sqrt{ a^2 + b^2 } = \sqrt{ 4^2 + 3^2 } = \sqrt{ 16 + 9 } = \sqrt{ 25 } = 5 $$
E' la lunghezza del segmento (o vettore) che coingiunge l'origine O con il punto (4;3) del numero complesso sul piano di Gauss.
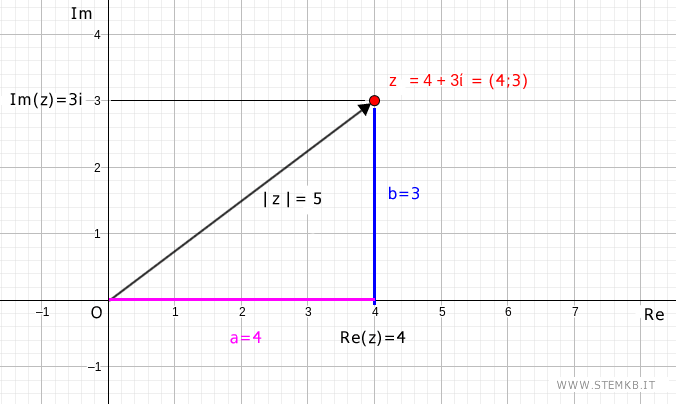
In conclusione, il modulo del numero complesso z=4+3i è uguale a |z|=5.

