Il numero complesso coniugato
Il numero complesso coniugato di un numero complesso z=a+bi è ottenuto cambiando il segno della parte immaginaria. $$ z' = a-bi $$
In genere, un numero complesso è scritto nella forma algebrica a + bi, dove "a" e "b" sono numeri reali e "i" è l'unità immaginaria che soddisfa la condizione i2 = -1.
$$ z = a+bi $$
Il suo numero complesso coniugato è z'=a-bi
$$ z' = a-bi $$
Ovviamente è una relazione in entrambi i versi. Quindi, se z' è il coniugato di z, allora z è il coniugato di z'.
Ad esempio, se il numero complesso è z=a-bi $$ z = a-bi $$ Il suo numero complesso coniugato è z'=a+bi, ossia un numero complesso con la stessa parte reale e la parte immaginaria opposta $$ z' = a+bi $$
Un esempio
Prendi come esempio il numero complesso z=3 + 4i
$$ z = 3+4i $$
Per ottenere il suo numero complesso coniugato, cambia il segno alla parte immaginaria (4i)
$$ z' = 3+4i $$
Quindi, il coniugato di z=3+4i è il numero complesso z'=3-4i
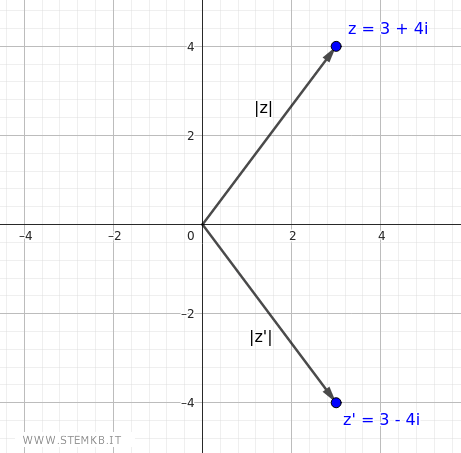
Perché si chiama numero complesso coniugato? Il coniugato di un numero complesso è legato al numero complesso originale attraverso la simmetria rispetto all'asse reale nel piano complesso. Se rappresenti il numero complesso z=3+4i e il suo coniugato z'=3-4i su un diagramma Argand-Gauss, un piano cartesiano in cui l'asse orizzontale rappresenta la parte reale e l'asse verticale rappresenta la parte immaginaria, i due numeri sono riflessi l'uno rispetto all'altro sull'asse reale. Quindi, il termine "coniugato" riflette questa relazione di simmetria tra un numero complesso e il suo coniugato.
Le proprietà dei numeri complessi coniugati
I numeri complessi coniugati hanno alcune proprietà particolari
- La somma di un numero complesso e del suo coniugato è un numero reale z+z'=2a
$$ z+z' = 2a $$
La somma di un numero complesso z=a+bi con il suo coniugato z'=a-bi è un numero reale z+z'=2a $$ z+z' = a+bi + a - bi = 2a $$ - La differenza tra un numero complesso e il suo coniugato è un numero immaginario z-z'=2bi
$$ z-z' = 2bi $$
La differenza tra un numero complesso z=a+bi e il suo coniugato z'=a-bi è un numero immaginario z-z'=2bi $$ z-z' = a+bi - (a - bi) = 2bi $$ - Il prodotto di un numero complesso con il suo coniugato è un numero reale z·z'=a2+b2
$$ z \cdot z' = a^2+b^2 $$
Il prodotto di un numero complesso z=a+bi con il suo coniugato z'=a-bi è un numero reale z·z'=a2+b2 $$ z \cdot z' = (a+bi) \cdot (a - bi) = a^2-abi+abi-b^2i^2 = a^2 - b^2 i^2 $$ Tu dovresti già sapere che il quadrato dell'unità immaginaria è i2=-1 $$ z \cdot z' = a^2 - b^2 i^2 = a^2 - b^2 \cdot (-1) = a^2+b^2 $$
A cosa serve il numero complesso coniugato?
Il coniugato di un numero complesso è un concetto molto utile in matematica e ingegneria perché ha diverse applicazioni pratiche.
Ad esempio, semplifica la divisione tra due numeri complessi.
Quando devi dividere due numeri complessi in forma algebrica z1/z2, moltiplica il numeratore e il denominatore per il coniugato del denominatore (z'2).
$$ \frac{z_1}{z_2} = \frac{z_1}{z_2} \cdot \frac{z'_2}{z'_2} $$
In questo modo il denominatore diventa un numero reale e il calcolo è molto più semplice.
Esempio. Considera i due numeri complessi $$ z_1 = 4+5i $$ $$ z_2 = 2+3i $$ Ora calcola la divisione tra i due numeri $$ \frac{z_1}{z_2} = \frac{4+5i}{2+3i} $$ Per semplificare il calcolo, moltiplica il numeratore e il denominatore per il coniugato del denominatore z'=2-3i $$ \frac{z_1}{z_2} = \frac{4+5i}{2+3i} \cdot \frac{2-3i}{2-3i} $$ Poi svolgi le moltiplicazioni al numeratore e al denominatore usando le regole tradizionali dell'algebra $$ \frac{z_1}{z_2} = \frac{8-12i+10i-15i^2}{4-6i+6i-9i^2} $$ $$ \frac{z_1}{z_2} = \frac{8-2i-15i^2}{4-9i^2} $$ Tu sai già che il quadrato dell'unità immaginaria i2=-1 è uguale a meno uno. $$ \frac{z_1}{z_2} = \frac{8-2i-15 \cdot (-1)}{4-9 \cdot (-1)} $$ $$ \frac{z_1}{z_2} = \frac{8-2i+15}{4+9} $$ $$ \frac{z_1}{z_2} = \frac{23-2i}{13} $$ $$ \frac{z_1}{z_2} = \frac{23}{13} - \frac{2}{13} i $$ Il risultato finale è il quoziente della divisione tra i due numeri complessi.
Inoltre, il coniugato di un numero complesso ti permette anche di calcolare il modulo del numero complesso.
Secondo il teorema di Pitagora, il modulo |z| di un numero complesso z = a + bi è dato dalla seguente formula
$$ |z| = \sqrt{a^2 + b^2} $$
A sua volta la somma a2+b2 è uguale al prodotto z·z' tra il numero complesso z e il suo coniugato z'
E' una delle proprietà dei numeri complessi coniugati.
$$ |z| = \sqrt{a^2 + b^2} = \sqrt{ z \cdot z' } $$
Quindi, il modulo di un numero complesso z lo puoi ottenere anche calcolando la radice quadrata del prodotto tra il numero complesso z e il suo coniugato z'.
Esempio. Considera il numero complesso $$ z_1 = 4+5i $$ Per ottenere il modulo del numero complesso, calcola la radice quadrata del prodotto tra il numero complesso z1=4+5i e il suo coniugato z1'=4-5i. $$ |z_1| = \sqrt{z_1 \cdot z_2} $$ $$ |z_1| = \sqrt{(4+5i) \cdot (4-5i)} $$ $$ |z_1| = \sqrt{16 - 20i + 20i +25i^2} $$ $$ |z_1| = \sqrt{16 - 25i^2} $$ Il quadrato dell'unità immaginaria è i2=-1 $$ |z_1| = \sqrt{16 - 25 \cdot -1 } = \sqrt{16+25} = \sqrt{41} $$ Il risultato finale è il modulo del numero complesso z1=4+5i. E' lo stesso risultato che avresti ottenuto usando il teorema di Pitagora dove a=4 e b=5 sono i coefficienti della parte reale e immaginaria del numero complesso z1=4+5i. $$ |z_1| = \sqrt{a^2 + b^2} = \sqrt{4^2 + 5^2} = \sqrt{16+25} = \sqrt{41} $$
Infine, qualche altra applicazione pratica dei numeri complessi coniugati.
- Se moltiplichi un numero complesso per il suo coniugato ottieni un numero reale. Questo è utile quando devi eliminare la parte immaginaria di un'espressione.
- In ingegneria elettrica e nei sistemi di controllo, il coniugato complesso è utilizzato per analizzare le funzioni di trasferimento e le risposte in frequenza dei sistemi.
- Nella fisica quantistica, l'uso del coniugato complesso è fondamentale per calcolare le probabilità a partire dalla funzione d'onda di un sistema.

