
I numeri complessi in forma esponenziale
I numeri complessi possono essere rappresentati anche in forma esponenziale o polare. $$ z = re^{iθ} $$
dove:
- "r" è il modulo (o l'ampiezza) del numero complesso, calcolato come √(a² + b²)
- "θ" è l'argomento (o la fase) del numero complesso, calcolato come arctan(b/a)
- "i" è l'unità immaginaria
- "e" è la base dei logaritmi naturali (e=2,7182...)
Dal punto di vista grafico un numero complesso in forma esponenziale si presenta in questo modo
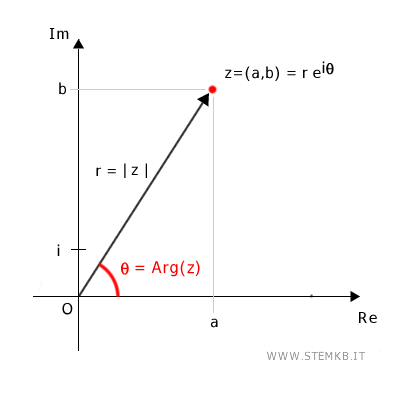
Perché rappresentare i numeri complessi in forma esponenziale? La forza esponenziale dei numeri complessi rende più semplice calcolare alcune operazioni come la divisione, la moltiplicazione tra numeri complessi, l'elevazione a potenza, la radice quadrata, ecc.
Ora ti spiego come si fa a ottenere questa formula.
Tu sai già che un numero complesso in forma cartesiana è rappresentato dalla formula
$$ z = a+bi $$
Dove "a" il coefficiente della parte reale, "b" è il coefficiente della parte immaginaria e "i" è l'unità immaginaria.
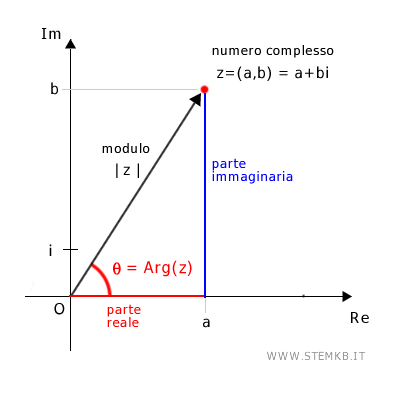
Lo stesso numero puoi rappresentarlo in forma trigonometrica in questo modo
$$ z = r \cdot ( \cos θ + i \cdot \sin θ ) $$
Dove "r" è il modulo e "θ" è l'argomento del numero complesso.
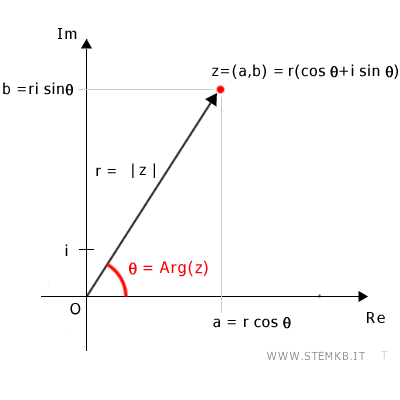
La formula di Eulero stabilisce una relazione tra la funzione esponenziale complessa eix e le funzioni trigonometriche
$$ e^{iθ} = \cos θ + i \cdot \sin θ $$
Sostituendo la formula di Eulero nella forma trigonometrica, ottieni la forma esponenziale di un numero complesso
$$ z = r \cdot ( \cos θ + i \cdot \sin θ ) $$
$$ z = r \cdot ( e^{iθ} ) $$
$$ z = r e^{iθ} $$
In questa rappresentazione, il modulo "r" rappresenta la distanza dal punto al centro del piano complesso e "θ" rappresenta l'angolo tra l'asse reale positivo e il punto nel piano complesso.

La forma esponenziale è molto utile per la moltiplicazione e la divisione di numeri complessi, poiché le operazioni diventano più semplici da eseguire.
Ad esempio, considera due numeri complessi in forma esponenziale
$$ z_1 = r_1 e^{iθ_1} $$
$$ z_2 = r_2 e^{iθ_2} $$
Per moltiplicare i due numeri devi semplicemente calcolare il prodotto dei moduli e la somma degli argomenti
$$ z_1 \cdot z_2 = (r_1 \cdot r_1) e^{i (θ_1+θ_1)} $$
Per dividere i due numeri, invece, ti basta calcolare il quoziente dei moduli e la differenza degli argomenti
$$ \frac{z_1}{z_2} = ( \frac{r_1}{r_2} ) e^{i (θ_1-θ_1)} $$
Per ottenere la potenza ennesima di un numero complesso, infine, devi calcolare la potenza ennesima del modulo e moltiplicare l'argomento per "n"
$$ z_1^n = ( z_1^n) e^{i (θ_1 \cdot n)} $$
Questo rende più semplice e intuitivo il calcolo delle principali operazioni matematiche con i numeri complessi.

