
I numeri complessi in forma trigonometrica
In questa lezione ti spiego come trasformare un numero complesso dalla forma algebrica alla forma trigonometrica (o polare)
Un numero complesso in forma trigonometrica si scrive in questo modo $$ z = r \cdot ( \cos \alpha + i \cdot \sin \alpha ) $$ Dove r è il modulo del numero complesso mentre alfa è l'argomento.
Ricorda che ogni numero complesso z=a+bi è un punto z=(a;b) sul piano di Gauss.
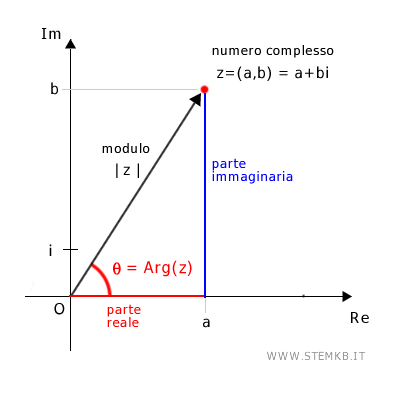
La magnitudine (o il modulo) del numero complesso z=a+bi è la lunghezza del vettore che congiunge l'origine con il punto associato al numero complesso.
Si può calcolare il teorema di Pitagora $$ r = \sqrt{a^2 + b^2} $$
L'argomento del numero complesso è l'angolo tra l'asse dei numeri reali positivi e il vettore. Lo puoi calcolare utilizzando l'arcotangente di b/a $$ θ = \arctan(b/a) $$
I numeri complessi in forma trigonometrica (polare) sono molto utili perché semplificano molte operazioni matematiche tra i numeri complessi. Inoltre, permettono la rappresentazione dei numeri complessi in forma esponenziale.
Un esempio
Ti faccio un esempio pratico
Disegna il numero complesso z1=4+3i sul piano di Gauss.
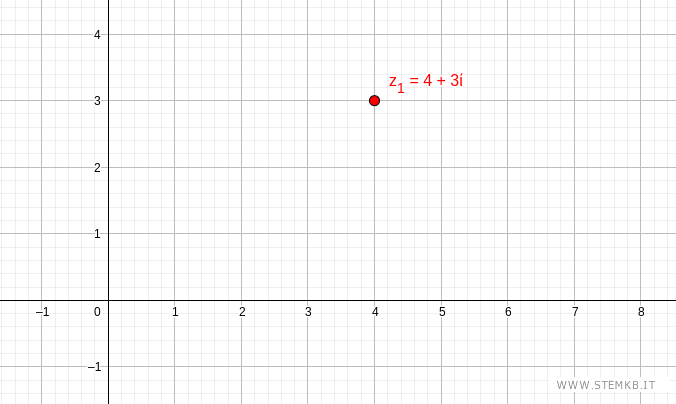
Il numero complesso si trova alle coordinate (4,3) del piano.
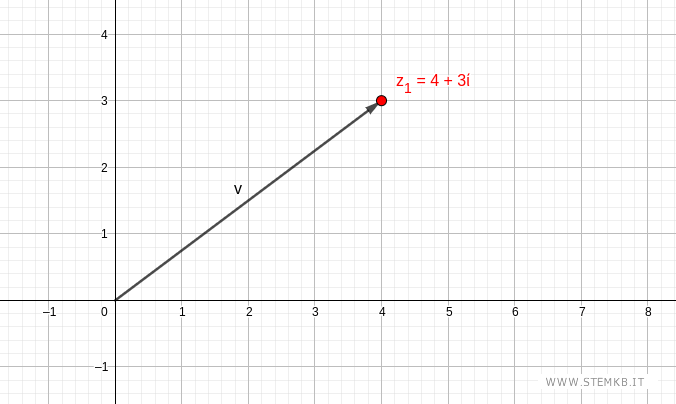
Ora traccia un vettore che collega l'origine (O) con il punto (4,3) sul piano.
La lunghezza del vettore è il modulo del numero complesso.
L'angolo alfa tra il vettore e il semiasse reale positivo è l'argomento del numero complesso.
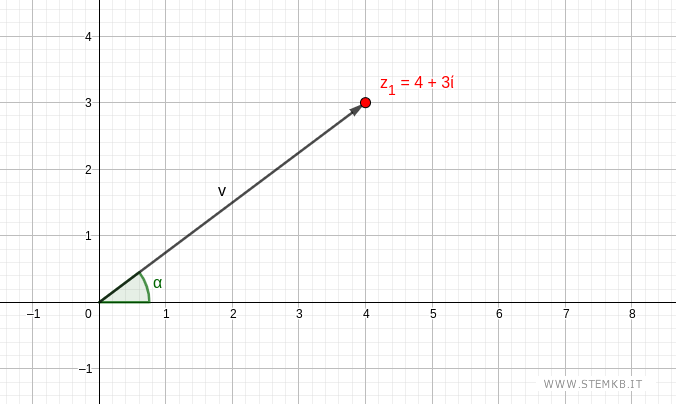
Ogni numero complesso del piano ha un modulo r e un argomento α.
Questa coppia di valori [r;α] indica le coordinate polari del numero complesso.
Come passare dalla forma algebrica a quella trigonometrica
Per passare dalla forma algebrica del numero complesso z=a+bi alla forma trigonometrica devi calcolare la lunghezza del modulo e l'angolo alfa dell'argomento.
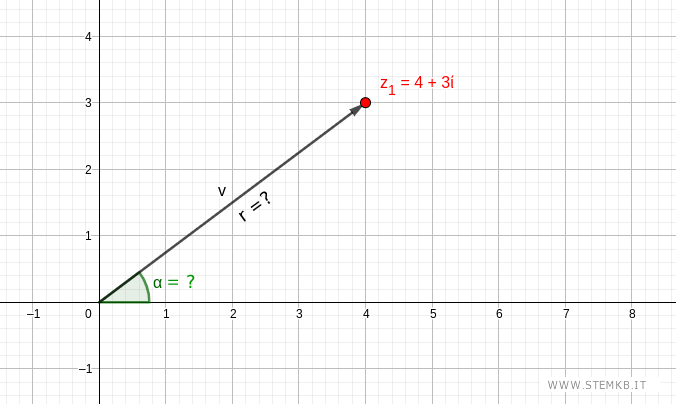
Il modulo puoi calcolarlo facilmente con il teorema di Pitagora.
Ad esempio, il numero complesso z1=4+3i forma un triangolo sul piano.
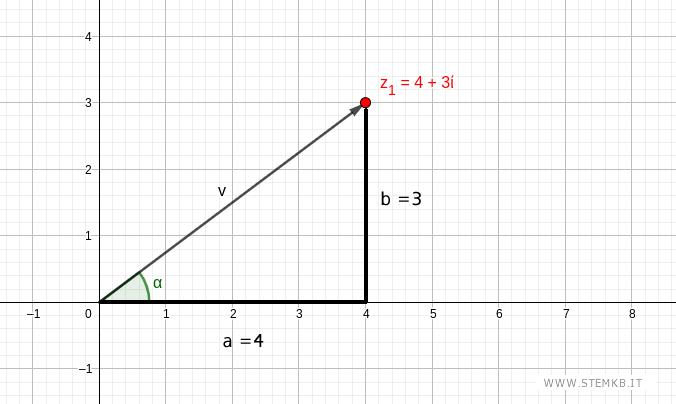
Il modulo è l'ipotenusa del triangolo mentre gli altri due lati (cateti) sono segmenti lunghi a=4 e b=3.
Secondo il teorema di Pitagora l'ipotenusa del triangolo è
$$ r = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5 $$
Quindi il modulo del numero complesso è r=5
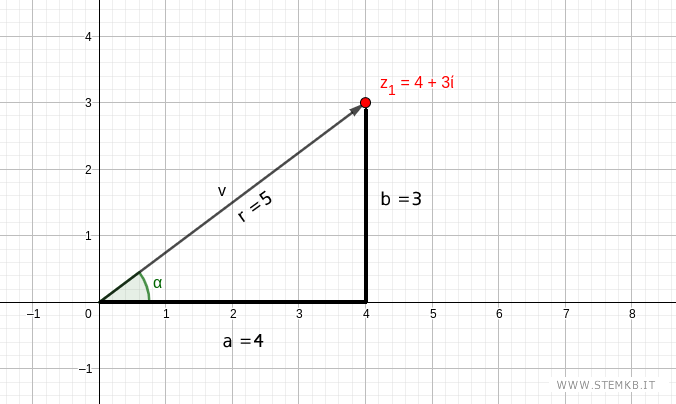
Per trovare l'angolo alfa (argomento) devi usare la trigonometria.
Puoi calcolarlo tramite l'arcotangente del rapporto b/a ossia 3/4.
$$ \alpha = \arctan ( \frac{b}{a} ) $$
$$ \alpha = \arctan ( \frac{3}{4} ) = 36.87° $$
Quindi l'argomento del numero complesso è a=36.87°
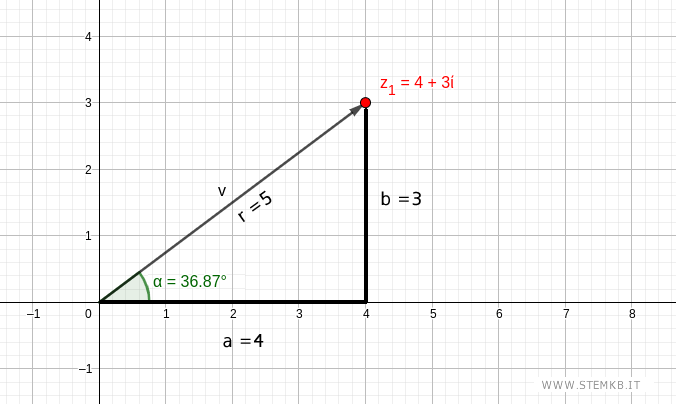
Metti insieme queste due informazioni e ottieni le coordinate polari del numero complesso z1
$$ z_1 = [ \ r \ ; \ \alpha \ ] = [ \ 5 \ ; \ 36.87° \ ] $$
A questo punto, una volta noto il modulo r=5 e l'argomento α=36.87°, puoi scrivere il numero complesso in forma trigonometrica
$$ z_1 = r \cdot ( \cos \alpha + i \cdot \sin \alpha ) $$
$$ z_1 = 5 \cdot ( \cos 36.87° + i \cdot \sin 36.87° ) $$
In conclusione, scrivere z1=4+3i oppure z1=5·[cos 36.87+i·sin 36.87°] è la stessa cosa.
Si tratta dello stesso numero complesso.
Come passare dalla forma trigonometrica a quella algebrica
Se hai un numero complesso in forma trigonometrica
$$ z = 5 \cdot ( \cos \alpha + i \cdot \sin \alpha ) $$
per tornare alla forma algebrica z=a+bi puoi usare queste due formule
$$ a= r \cdot \cos \alpha $$
$$ b= r \cdot \sin \alpha $$
Ad esempio se il modulo è r=5 e l'argomento è α=36.87°
$$ a= 5 \cdot \cos 36.87° = 4$$
$$ b= 5 \cdot \sin 36.87° = 3 $$
il numero complesso in forma algebrica si trova alle coordinate (a;b)=(3;4) ossia z1=3+4i.
Perché utilizzare i numeri complessi in forma polare?
La rappresentazione polare dei numeri complessi è molto utile in molte applicazioni, perché molte operazioni matematiche tra numeri complessi sono più semplici da calcolare se i numeri complessi sono in forma polare piuttosto che in forma cartesiana.
Ad esempio, considera due numeri complessi in forma polare.
$$ z_1 = r_1(\cos(θ_1) + i \cdot \sin(θ_1)) $$
$$ z_2 = r_2(\cos(θ_2) + i \cdot \sin(θ_2)) $$
Il prodotto tra due numeri complessi in forma polare si ottiene semplicemente moltiplicando i loro moduli e sommando i loro argomenti.
$$ z_1 \cdot z_2 = r_1 \cdot r_2 ( \cos(θ_1+θ_2) + i \cdot \sin(θ_1+θ_2)) $$
La divisione si esegue in modo simile, devi dividere i moduli e calcolare la differenza tra i loro argomenti.
$$ \frac{z_1}{z_2} = \frac{r_1}{r_2} ( \cos(θ_1-θ_2) + i \cdot \sin(θ_1-θ_2)) $$
Inoltre, la forma polare è il punto di partenza per la forma esponenziale dei numeri complessi, grazie alla formula di Eulero.
Se questa lezione online di StemKB ti piace, continua a seguirci.

