L'unità immaginaria dei numeri complessi
L'unità immaginaria dei numeri complessi è un concetto fondamentale nel campo dei numeri complessi. È rappresentata dal simbolo "i", oppure "j", e la sua caratteristica distintiva è che quando viene elevata al quadrato, il risultato è -1. In altre parole $$ i^2 = -1 $$
L'unità immaginaria è la pietra angolare dei numeri complessi, un'estensione del campo dei numeri reali che include numeri "immaginari".
Un numero complesso (z) è generalmente espresso nella forma a + bi, dove a e b sono numeri reali, e "i" è l'unità immaginaria.
$$ z = a+bi $$
La parte "a" è chiamata parte reale, mentre "b" è la parte immaginaria del numero complesso.
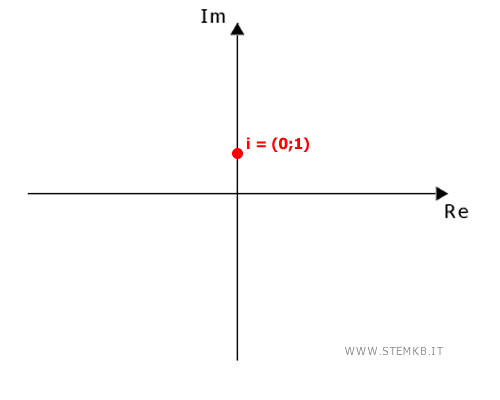
L'unità immaginaria "i" si trova sul piano complesso al punto (0;1), che corrisponde a un raggio di 1 e un angolo di π/2 in coordinate polari.
L'unità immaginaria è legata anche all'identità di Eulero, una delle più belle equazioni della matematica. $$ e^{πi} = -1 $$ L'identità di Eulero collega cinque dei più importanti simboli matematici: e, π, i, 1, e 0.
A cosa serve l'unità immaginaria?
L'unità immaginaria ti permette di calcolare la radice quadrata anche dei numeri negativi.
Ad esempio, immagina di avere la radice quadrata di -25
$$ \sqrt{-25} $$
Puoi scrivere il radicando in questo modo equivalente -1·25
$$ \sqrt{-1 \cdot 25} $$
Ora, per definizione il quadrato dell'unità immaginaria è -1, ossia i2=-1
Quindi, puoi sostituire -1 con i2
$$ \sqrt{i^2 \cdot 25} $$
In questo modo puoi far uscire l'unità immaginaria "i" dalla radice
$$ i \cdot \sqrt{25} $$
Adesso il radicando è un numero positivo e puoi calcolare la radice quadrata di 25 che è uguale a 5
$$ i \cdot 5 $$
In conclusione, la radice quadrata di -25 è il numero immaginario 5i ossia il numero complesso z=0+5i
$$ \sqrt{-25} = 5i = 0+5i $$
L'idea di numeri immaginari e complessi può sembrare estranea e inutile a prima vista. Dopotutto, come può un numero la cui quadratura è negativa avere un significato o un'utilità nel mondo reale? Tuttavia, i numeri complessi hanno trovato applicazioni in una vasta gamma di campi, dalla fisica alla ingegneria elettrica, dalla teoria dei segnali alla meccanica quantistica.

