
Come sommare i vettori
In questa lezione ti spiego come sommare due o più vettori in algebra lineare con un semplice esempio pratico.
Dati due vettori $$ \vec{v_1} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \\ \vec{v_2} = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} $$ la somma dei vettori è un vettore che ha per componenti la somma delle componenti di v e w. $$ \vec{v_1} + \vec{v_2} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} x_1+x_2 \\ y_1+y_2 \end{pmatrix} $$
Ad esempio, hai due vettori
$$ \vec{u} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} \\ \vec{v} = \begin{pmatrix} 5 \\ 1 \end{pmatrix} $$
I due vettori si presentano in questo modo sul piano cartesiano.
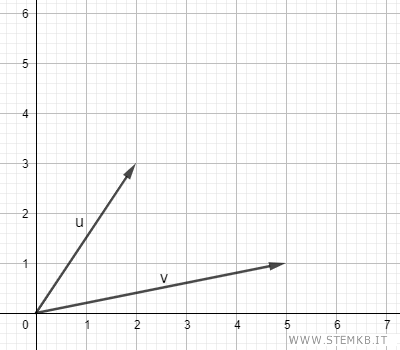
Per calcolare la somma dei due vettori, devi sommare le componenti dei due vettori.
$$ \vec{u} + \vec{v} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} + \begin{pmatrix} 5 \\ 1 \end{pmatrix} = \begin{pmatrix} 2+5 \\ 3+1 \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix}$$
Quindi il vettore somma è
$$ \vec{u} + \vec{v} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} $$
Ecco come si presenta il vettore somma sul piano cartesiano.
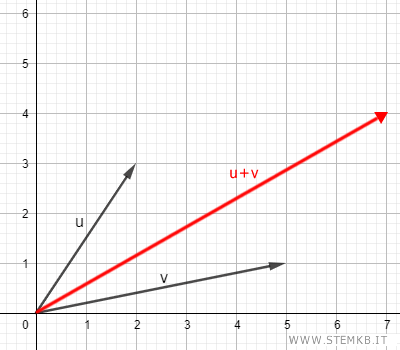
Se i vettori hanno due componenti, puoi realizzare la somma anche geometricamente con il metodo del parallelogramma oppure con il metodo punta-coda.
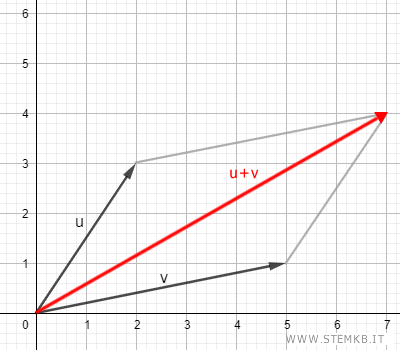
Nota. La lunghezza (modulo o norma) del vettore somma è sempre inferiore o uguale alla somma della lunghezza dei vettori che hai sommato. $$ | \vec{v_1} + \vec{v_1} | \le |\vec{v_1}|+|\vec{v_2}| $$ Questa proprietà della somma dei vettori è detta disuguaglianza triangolare. La lunghezza del vettore somma è uguale alla somma delle lunghezze dei vettori solo quando i vettori hanno la stessa direzione e verso oppure almeno uno dei due è un vettore nullo.
Come sommare più vettori?
Il metodo di calcolo è sempre lo stesso.
Ad esempio, hai tre vettori
$$ \vec{u} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} \\ \vec{v} = \begin{pmatrix} 5 \\ 1 \end{pmatrix} \\ \vec{w} = \begin{pmatrix} -1 \\ 1 \end{pmatrix} $$
Il vettore somma è il vettore composto dalla somma algebrica delle componenti dei tre vettori.
$$ \vec{u} + \vec{v} + \vec{w} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} + \begin{pmatrix} 5 \\ 1 \end{pmatrix} + \begin{pmatrix} -1 \\ 1 \end{pmatrix} = \begin{pmatrix} 2+5+(-1) \\ 3+1+1 \end{pmatrix} = \begin{pmatrix} 6 \\ 5 \end{pmatrix} $$
E se i vettori hanno più di due componenti?
Il metodo è sempre lo stesso. Il vettore somma è un vettore con la somma delle tre componenti.
Ad esempio, hai due vettori con tre componenti ciascuno.
$$ \vec{u} = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} \\ \vec{v} = \begin{pmatrix} 5 \\ 1 \\ 4 \end{pmatrix} $$
La somma dei due vettori è
$$ \vec{u} + \vec{v} = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} + \begin{pmatrix} 5 \\ 1 \\ 4 \end{pmatrix} = \begin{pmatrix} 2+5 \\ 3+1 \\ 1+4 \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \\ 5 \end{pmatrix} $$
Se questa lezione di StemKB ti piace, continua a seguirci.

