Il complementare di un insieme

Dato un insieme $ B $, sottoinsieme di un insieme più grande $ A $, si chiama complementare di $ B $ rispetto ad $ A $ l'insieme degli elementi che appartengono ad $ A $ ma non a $ B $. In simboli, si scrive: \[C_A(B) = A - B\] oppure più semplicemente: \[ \overline{B}_A = A - B \]
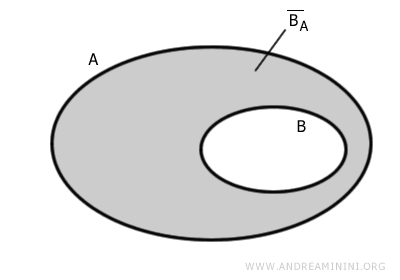
esempio di insieme complementare

Nella teoria degli insiemi, il concetto di complementare di un insieme è fondamentale per descrivere tutto ciò che "manca" rispetto a un insieme dato.

Ma cosa significa esattamente complementare di un insieme? Scopriamolo con una definizione chiara ed esempi pratici.

Se consideri l'insieme universo $ U $, ovvero l'insieme che contiene tutti gli elementi di riferimento del problema, il complementare di un insieme $ A $ rispetto a $ U $ è l'insieme degli elementi che appartengono a $ U $ ma non ad $ A $. Questo si indica con il simbolo $ A^C $ o $ \overline{A} $, quindi: \[ A^C = U - A \] In altre parole, il complementare di un insieme è tutto ciò che "resta fuori" rispetto all'insieme universo di riferimento.

Esempi pratici

Per comprendere meglio il concetto, vediamo alcuni esempi.

Immaginiamo di avere un insieme universo $ U $, che rappresenta tutti gli studenti di una scuola. Supponiamo che nella scuola ci siano 100 studenti

$$ U = 100 $$

All'interno di questa scuola, consideriamo l'insieme $ A $, che raccoglie gli studenti che praticano sport.

Ad esempio, 60 studenti praticano uno sport

$$ A = 60 $$

Ora, vogliamo determinare il complementare di $ A $ rispetto a $ U $, ovvero l'insieme degli studenti che non praticano sport.

$$ A^C = U - A = 100 - 60 = 40 $$

Quindi, il complementare di $ A $ è l'insieme formato da 40 studenti che non fanno attività sportiva.

Questo esempio mostra come il complementare di un insieme aiuti a identificare ciò che non rientra in una certa categoria.