La differenza simmetrica tra insiemi

La differenza simmetrica tra due insiemi A e B è un insieme di elementi che appartengono a uno degli insiemi ma non appartengono a entrambi. $$ (A - B) ∪ (B - A) $$

In altre parole, la differenza simmetrica tra A e B è composta dagli elementi presenti in A che non sono presenti in B, e dagli elementi presenti in B che non sono presenti in A.

Ti faccio un esempio pratico.

Immagina due insiemi finiti A e B con questi elementi

$$ A = \{ 1, 2, 3 \} $$

$$ B = \{ 2, 3, 4 \} $$

La differenza simmetrica tra questi insiemi è un insieme composto dagli elementi 1 e 4

$$ (A - B) ∪ (B - A) = \{ 1, 4 \}$$

L'elemento 1 è presente nell'insieme A ma non in B.

L'elemento 4 è presente nell'insieme B ma non in A.

Gli altri elementi 2, 3 sono presenti in entrambi gli insiemi e vanno eliminati.

Prova a disegnare i due insiemi A e B con i diagrammi di Eulero-Venn.

 

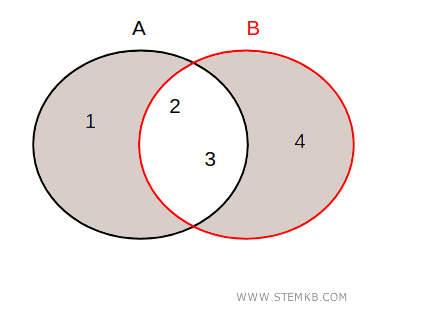
La differenza simmetrica tra i due insiemi sono le zone che non si intersecano.