L'insieme delle parti

L'insieme delle parti di un insieme $ X $ è l'insieme di tutti i possibili sottoinsiemi di quell'insieme, inclusi il sottoinsieme vuoto e l'insieme stesso.  Si indica con  $ P(X) $.

E' anche detto insieme potenza.

Se un insieme \( A \) ha \( n \) elementi, allora l'insieme delle parti di \( A \) ha \( 2^n \) elementi. Questo perché ogni elemento può essere presente o assente in ogni sottoinsieme, il che crea \( 2 \) scelte per ogni elemento.

La funzione che associa ad ogni insieme la cardinalità del suo insieme delle parti è una funzione esponenziale nella teoria dei numeri. Questo dimostra che l'insieme delle parti ha una crescita molto rapida all'aumentare della cardinalità dell'insieme originale.

L'insieme delle parti è usato per definire relazioni e funzioni in matematica, particolarmente nelle definizioni formali di relazioni binarie e funzioni come particolari sottoinsiemi di prodotti cartesiani.

Esempio

Prendiamo un insieme composto da n=2 elementi.

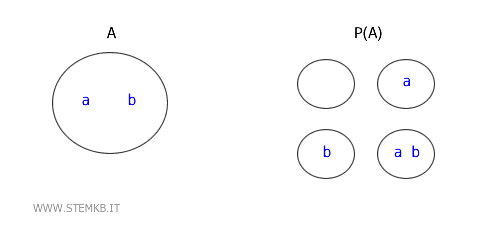
$$ A = \{a, b\}  $$

L'insieme delle parti di \( A \) è composto da 2²=4 insiemi

$$ P(A) = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} $$

Esempio 2

Se prendiamo un altro insieme molto semplice ma con n=3 elementi come:

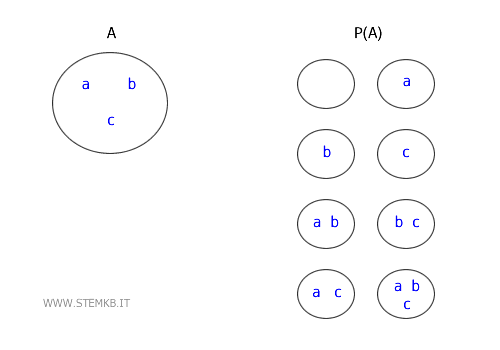
$$ A = \{a, b, c\} $$

L'insieme delle parti $ P(A) $ è composto da 2³=8 sottoinsiemi.

$$ \mathcal{P}(A) = \{\emptyset, \{a\}, \{b\}, \{c\}, \{ab\}, \{ac\}, \{bc\}, \{a, b, c\}\} $$

In contesti più complessi, il numero dei sottoinsiemi cresce in modo esponenziale con la cardinalità dell'insieme iniziale.

Esempio 3

Consideriamo un insieme composto da n=4 elementi.

$$ A = \{a, b, c, d\} $$

In questo caso l'insieme delle parti P(A) è composto da 2⁴=16 sottoinsiemi.

1. \( \emptyset \)
2. \( \{a\} \)
3. \( \{b\} \)
4. \( \{c\} \)
5. \( \{d\} \)
6. \( \{a, b\} \)
7. \( \{a, c\} \)
8. \( \{a, d\} \)
9. \( \{b, c\} \)
10. \( \{b, d\} \)
11. \( \{c, d\} \)
12. \( \{a, b, c\} \)
13. \( \{a, b, d\} \)
14. \( \{a, c, d\} \)
15. \( \{b, c, d\} \)
16. \( \{a, b, c, d\} \)

Questi sottoinsiemi rappresentano tutte le possibili combinazioni degli elementi di \( A \), inclusi l'insieme vuoto e l'insieme completo.