Le sequenze o tuple

Una sequenza è una collezione ordinata di oggetti, dove l'ordine degli elementi è significativo.

In genere, le sequenze si rappresentano con gli elementi racchiusi tra parentesi tonde. Ad esempio, la sequenza dei numeri 8, 12 e 7 si scrive come \( (8, 12, 7) \).

Le sequenze possiedono due caratteristiche fondamentali:

• Ordine degli elementi: L'ordine in una sequenza è cruciale.

  Ad esempio, \( (1, 2, 3) \) è diverso da \( (3, 2, 1) \). Basta pensare a una password: invertire i caratteri la rende inutilizzabile.

• Ripetizione degli elementi: In una sequenza gli elementi possono ripetersi, e la ripetizione conta.

  Ad esempio, \( (1, 1, 2, 3) \) è diverso da \( (1, 2, 3) \). Immaginate di scrivere la stessa parola due volte in una frase: cambia il significato.

Come vedremo gli insiemi e le sequenze spesso si rappresentano allo stesso modo ma non sono la stessa cosa.

Tipi di sequenze

Le sequenze possono essere finite o infinite:

• Sequenze finite
  Hanno un numero limitato di elementi. Ecco un esempio di sequenza finita: \( (a, b, c) \).
• Sequenze infinite
  Hanno un numero illimitato di elementi, spesso rappresentate con puntini di sospensione. Immaginate i numeri naturali: non finiscono mai. Ad esempio, la sequenza infinita dei numeri dispari si scrive come \( (1, 3, 5, \ldots) \).

Le tuple o n-ple

Una sequenza finita con \( n \) elementi è chiamata tupla o n-upla (ennupla).

A seconda del numero degli elementi una tupla è detta:

• 1-upla (o singoletto): Una tupla con un solo elemento, es. \( (x) \).
• 2-upla (o coppia ordinata): Una tupla con due elementi, es. \( (x, y) \).
• 3-upla (o tripla): Una tupla con tre elementi, es. \( (x, y, z) \).
• k-upla: Una tupla con \( k \) elementi.

Ad esempio, una 4-upla contiene esattamente quattro elementi, come \( (a, b, c, d) \).

Il prodotto cartesiano e le sequenze

Il prodotto cartesiano è un concetto che produce coppie ordinate o tuple combinando elementi di due o più insiemi.

Sebbene non sia una sequenza, il prodotto cartesiano genera collezioni ordinate di elementi.

Ad esempio, il prodotto cartesiano degli insiemi \( A \) e \( B \), indicato come \( A \times B \), è composto da tutte le coppie ordinate \((a, b)\) dove \( a \in A \) e \( b \in B \).

Queste coppie ordinate possono essere viste come sequenze di lunghezza due.

Un altro esempio pratico di coppie ordinate sono le coordinate dei punti (x;y) sul piano cartesiano.

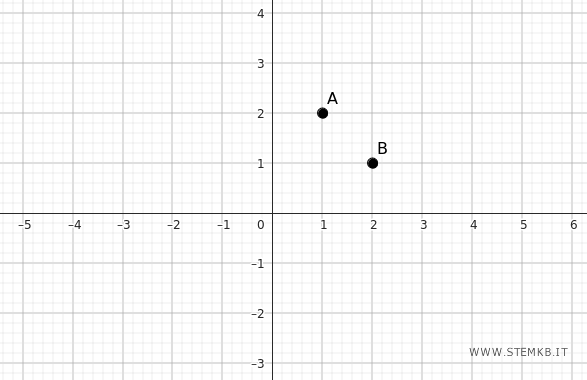
Come si può facilmente vedere, il punto alle coordinate (1;2) non occupa la stessa posizione del punto alle coordinate (2;1)

Le differenze tra insiemi e sequenze

La differenza principale tra insiemi e sequenze è l'importanza dell'ordine e della ripetizione degli elementi:

In un insieme l'ordine e la ripetizione non contano.

Ad esempio, l'insieme dei numeri \( \{a, b, c\} \) rimane invariato indipendentemente dall'ordine \( \{b, a, c\} \) o \( \{c, a, b\} \). Quando si raccoglie la frutta in un cesto, non conta la sequenza ma il contenuto.

In una sequenza, invece, l'ordine e la ripetizione sono fondamentali.

Ad esempio, le sequenze \( \{a, b, c\} \) e \( \{b, a, c\} \) sono diverse.  E' come seguire le istruzioni per montare un mobile, devono essere seguite in ordine preciso. Per fare una torta, bisogna seguire una sequenza, non un insieme di ingredienti a caso!

In conclusione, spesso le sequenze e gli insiemi sono rappresentati allo stesso modo, con le parentesi tonde, ma il significato è completamente diverso.