
I sottoinsiemi
Un sottoinsieme è un insieme i cui elementi appartengono tutti a un altro insieme, chiamato insieme di appartenenza.
In altre parole, un sottoinsieme è interamente contenuto (o incluso) in un altro insieme più grande.
Nota che un insieme può essere definito sottoinsieme di un altro solo se tutti i suoi elementi appartengono anche a quest'ultimo. Se anche solo un elemento non appartiene, non si può parlare di sottoinsieme.
Un esempio pratico
Ti faccio un esempio pratico.
Se A è un insieme che contiene elementi come 1, 2, 3 e 4
$$ A = \{ 1,2,3,4 \} $$
allora l'insieme B = {1, 2} è un sottoinsieme di A, perché ogni elemento di B appartiene anche a A.
$$ B = \{ 1,2 \} $$
In questo caso, l'insieme A è l'insieme di appartenenza e l'insieme B è il sottoinsieme.
Se rappresenti i due insiemi tramite i diagrammi di Venn, l'area del sottoinsieme B è completamente contenuta nell'area dell'insieme di appartenenza A.
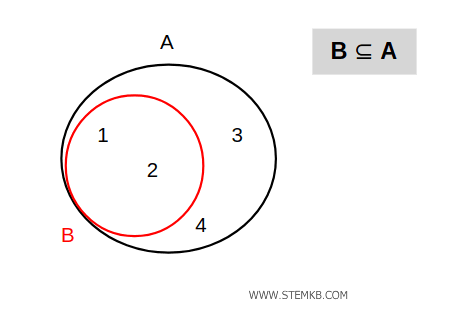
La relazione tra un insieme e il suo sottoinsieme si rappresenta con il simbolo di inclusione B ⊆ A.
Signfica che l'insieme B è contenuto nell'insieme A.
$$ B \subseteq A $$
In alternativa, puoi scrivre anche A ⊇ B. Vuol dire che l'insieme A contiene l'insieme B. $$ A \supseteq B $$ E' la stessa cosa ma vista da un punto di vista diverso.
Puoi usare questi simboli anche per scrivere relazioni tra più insiemi.
Ad esempio se A ⊇ B e B ⊇ C, allora A ⊇ C.
$$ A \supseteq B \supseteq C $$
Questo significa che se B è un sottoinsieme di A e C è un sottoinsieme di B, allora C è anche un sottoinsieme di A.
La relazione di inclusione stretta
L'inclusione stretta descrive un tipo di relazione tra due insiemi.
Un insieme A è incluso strettamente in un altro insieme B se tutti gli elementi di A sono anche elementi di B, ma A non è identico a B. $$ A \subseteq B \wedge A \ne B $$
Questa relazione viene indicata con il simbolo ⊂.
Ti faccio un esempio pratico.
Considera due insiemi A e B
$$ A = \{ 1,2, 3, 4 \} $$
$$ B = \{ 1,2 \} $$
L'insieme B è incluso strettamente in A perché tutti gli elementi di B sono anche elementi di A ma gli insiemi A e B non sono uguali.
$$ B \subset A $$
In questo caso si dice che B è un sottoinsieme in senso stretto di A.
In alternativa, si può dire anche che B è un sottoinsieme proprio di A.
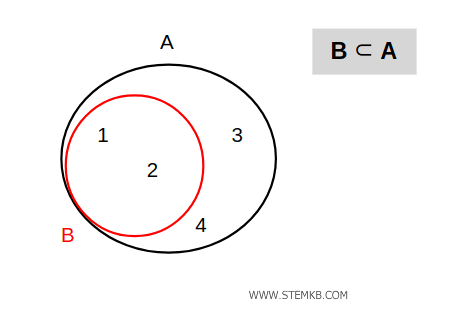
In questo caso particolare valgono entrambe le relazioni di inclusione. $$ B \subset A $$ $$ B \subseteq A $$
Se invece consideri il caso di due insiemi uguali $$ A = \{ 1,2, 3, 4 \} $$ $$ C = \{ 1,2,3,4 \} $$ puoi affermare solo che C è un sottoinsieme di A perché tutti gli elementi di C appartengono anche all'insieme A $$ C \subseteq A $$ Non puoi affermare che C è un sottoinsieme in senso stretto di A perché i due insiemi sono uguali $$ C \require{cancel} \cancel{ \subset } A $$ 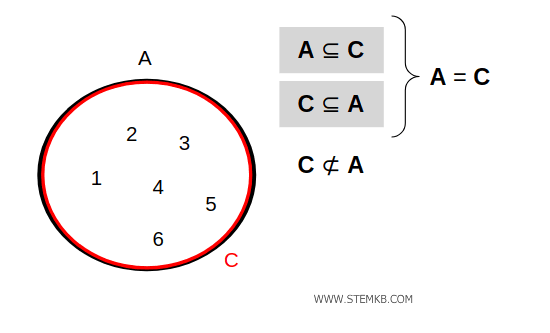
La differenza tra i simboli di inclusione e di appartenenza
Quando si affronta lo studio della matematica, soprattutto nella teoria degli insiemi, è fondamentale comprendere e distinguere correttamente i simboli di inclusione ($\subset$, $\subseteq$, $\not\subset$) e quelli di appartenenza ($\in$, $\not\in$).
I simboli di appartenenza $\in$ e $\not \in$ descrivono la relazione tra un elemento e un insieme.
Si utilizzano per indicare se un elemento appartiene o meno a un insieme.
Se un elemento $x$ è contenuto in un insieme $A$, si scrive: $$ x \in A $$
Se invece $x$ non è contenuto in $A$, si scrive: $$ x \not\in A $$
Ad esempio, il numero $3$ appartiene all'insieme dei numeri naturali. $$3 \in \mathbb{N}$$ Il numero $-2$ non appartiene all'insieme dei numeri naturali. $$-2 \not\in \mathbb{N} $$ Bisogna però fare attenzione, scrivere $ \{3\} \in \mathbb{N}$ non è corretto, perché $\{3\}$ è un insieme e non un singolo elemento.
I simboli di inclusione $\subset$, $\subseteq$ , $\not\subset$ e $\not\subseteq $ descrivono una relazione tra due insiemi.
Questi simboli indicano se un insieme è contenuto in un altro, cioè se tutti gli elementi del primo insieme sono anche elementi del secondo.
Ad esempio, l'insieme $\{1, 2\}$ è un sottoinsieme dei numeri naturali. $$\{1, 2\} \subseteq \mathbb{N}$$ L'insieme $\{1, 2\}$ è un sottoinsieme proprio di $\{1, 2, 3\}$ $$\{1, 2\} \subset \{1, 2, 3\}$$ Un errore comune è scrivere $-2 \subseteq \mathbb{Z}$ perché $-2$ è un elemento, non un insieme. Un altro errore comune è dire che $\mathbb{N} \in \mathbb{Z}$ non è corretto: $\mathbb{N}$ è un insieme e non un elemento di $\mathbb{Z}$. In questo caso, è appropriato usare il simbolo $\subseteq$.
Quindi, bisogna tenere a mente le differenze tra questi simboli.
| Simbolo | Relazione | Esempio corretto |
|---|---|---|
| \(\in\) | Elemento in un insieme | \(3 \in \mathbb{N}\) |
| \(\not\in\) | Elemento non in un insieme | \(-2 \not\in \mathbb{N}\) |
| \(\subset\) | Insieme in un insieme (proprio) | \(\{1, 2\} \subset \{1, 2, 3\}\) |
| \(\subseteq\) | Insieme in un insieme (anche uguale) | \(\{1, 2\} \subseteq \mathbb{N}\) |
| \(\not\subset\) | Insieme non incluso | \(\{-1, 0\} \not\subset \mathbb{N}\) |
Quindi, per utilizzare correttamente i simboli di appartenenza e inclusione, è cruciale ricordare che $\in$ e $\not\in$ si riferiscono a elementi e $\subset$ e $\subseteq$ si riferiscono a insiemi.
I sottoinsiemi impropri
Tutti gli insiemi hanno sempre almeno due sottoinsiemi detti sottoinsiemi impropri
- L'insieme vuoto (o insieme nullo)
L'insieme vuoto è un sottoinsieme improprio di qualsiasi altro insieme. Un insieme è detto insieme vuoto Ø se e solo se non contiene alcun elemento. $$ Ø \subseteq A $$Esempio. L'insieme vuoto Ø={ } è un sottoinsieme improprio dell'insieme A ossia Ø⊆A $$ Ø \subseteq \{1, 2, 3, 4 \} $$
- L'insieme uguale
L'insieme uguale è un altro sottoinsieme improprio. Ogni insieme ha come sottoinsieme improprio l'insieme uguale a se stesso. $$ A \subseteq A $$Esempio. L'insieme A={1,2,3,4} ha come sottoinsieme improprio l'insieme uguale a se stesso A={1,2,3,4] ossia A⊆A $$ \{ 1,2,3,4 \} \subseteq \{ 1,2,3,4 \} $$
In alcuni libri di matematica viene considerato sottoinsieme improprio soltanto l'insieme uguale a se stesso, ma non l'insieme vuoto, a seconda della definizione di "sottoinsieme proprio" che viene adottata.

