Gli insiemi

Un insieme è un raggruppamento di oggetti distinti, detti elementi, che condividono una certa proprietà in comune.

Gli oggetti presenti in un insieme sono chiamati elementi dell'insieme.

Per definire un insieme devi prima stabilire un criterio di appartenenza all'insieme.

Cos'è il criterio di appartenenza?

Il criterio di appartenenza è una regola che permette di capire con certezza se un oggetto appartiene all'insieme oppure no. 

In matematica, si considerano insiemi esclusivamente quei raggruppamenti di elementi per i quali è possibile determinare, attraverso un criterio oggettivo, se un oggetto appartiene o meno al raggruppamento.

Esempio: Non è possibile definire l'insieme delle persone alte in una scuola senza specificare cosa si intende per "alto". Una persona è considerata alta se supera i 170 cm? Oppure i 180 cm? ecc. È indispensabile stabilire un criterio oggettivo di selezione.

Come si rappresenta un insieme?

Un modo per rappresentare un insieme consiste nell'inserire la lista degli elementi tra due parentesi graffe. Questa notazione è particolarmente utile per gli insiemi finiti.

Ad esempio, l'insieme delle vocali è composto dalle lettere a,e,i,o,u

$$ vocali = \{ \ a \ , \ e \ , \ i \ , \ o \ , \ u \ \} $$

Le lettere sono gli elementi dell'insieme "vocali".

Questo insieme è anche detto insieme finito perché è composto da un numero finito di elementi.

Un altro esempio è l'insieme dei numeri pari da 1 a 10.

$$ P = \{ \ 2 , 4, 6, 8, 10 \ \} $$

I numeri pari sono gli elementi dell'insieme P.

Attenzione. Il criterio di appartenenza non deve essere soggettivo. Deve permettere a chiunque di stabilire con certezza se un oggetto appartiene all'insieme oppure no. Ad esempio, i film divertenti non sono un insieme perché un film che tu giudichi divertente, potrebbe non esserlo per i tuoi amici o per altre persone.

Se vogliamo indicare l'insieme dei numeri pari compresi tra 1 e 10 (incluso), possiamo scriverlo in modo più rigoroso tramite la proprietà caratteristica, ossia la regola che decide quali oggetti appartengono all'insieme e quali no.

Ad esempio, per indicare i numeri pari da 1 a 10 possiamo scrivere

$$ P = \{x \in \mathbb{N} \mid x \text{ è pari e } 1 \leq x \leq 10\} $$

Qui, il simbolo \( \mid \) (o \( : \), a seconda delle preferenze) indica "tale che", e la condizione logica specifica sia che \( x \) è un numero pari, sia che appartiene all'intervallo desiderato.

Possiamo rappresentare graficamente gli insiemi utilizzando i diagrammi di Eulero-Venn.

In questi diagrammi, ogni insieme è rappresentato da una linea chiusa, non intrecciata, che racchiude al suo interno i punti corrispondenti agli elementi dell'insieme.

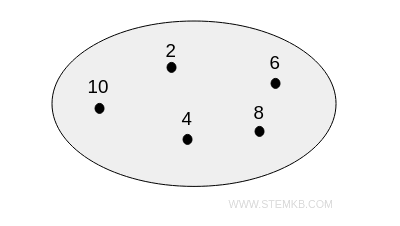
I diagrammi di Eulero-Venn sono molto utili per rappresentare in modo visivo le relazioni tra insiemi, come intersezioni, unioni e differenze.

Tuttavia, non conviene usarli quando si tratta di insiemi più complessi o con numerosi elementi.

Qual è lo strumento migliore? La scelta del metodo più adatto dipende dalla complessità dell'insieme e dallo scopo dell'analisi. Ogni metodo ha pro e contro ed è vantaggioso in contesti specifici. La rappresentazione per elencazione è chiara e semplice da utilizzare per insiemi piccoli, ma diventa inefficace per insiemi grandi o infiniti. La proprietà caratteristica consente una descrizione sintetica e utile per insiemi infiniti, ma è necessario che esista una formula logica per definire l'appartenenza e non sempre è facile. Inoltre,  richiede familiarità con il linguaggio matematico ed è meno intuitiva. I diagrammi di Eulero-Venn offrono una visualizzazione intuitiva delle relazioni tra insiemi, ma sono limitati a pochi insiemi o a relazioni semplici.

Quali sono le caratteristiche di un insieme?

Un insieme ha due caratteristiche

• In un insieme gli elementi sono distinti l'uno dall'altro. Ogni elemento in un insieme deve essere unico. In altre parole, non possono esserci duplicati. Se un elemento già appartiene all'insieme, non può apparire due o più volte nello stesso insieme. Ad esempio, nell'insieme delle vocali non puoi inserire la lettera 'a' due volte. $$ vocali = \{ \ a \ , \ \color{red}a \ , \ e \ , \ i \ , \ o \ , \ u \ \} $$
• Un'altra particolarità degli insiemi è che non c'è un ordine degli elementi. L'ordine degli elementi in un insieme non ha alcuna importanza. Ad esempio, l'insieme delle vocali puoi scriverlo anche in questi modi. $$ vocali = \{ \ u \ , \ o \ , \ i \ , \ e \ , \ a \ \} $$ $$ vocali = \{ \ i \ , \ u \ , \ e \ , \ a \ , \ o \ \} $$ $$ vocali = \{ \ e \ , \ a \ , \ u \ , \ o \ , \ i \ \} $$ Anche se la disposizione degli elementi cambia, è sempre lo stesso insieme perché gli elementi sono gli stessi.

Qual è il simbolo di un insieme?

In matematica gli insiemi sono indicati con le lettere maiuscole dell'alfabeto A,B,C,... , mentre gli elementi con le lettere minuscole a,b,c,...

Ad esempio, scrivi l'insieme delle vocali con la lettera A e l'insieme delle consonanti con la lettera B $$ A = \{ \ u \ , \ o \ , \ i \ , \ e \ , \ a \ \} $$ $$ B = \{ \ b \ , \ c \ , \ d \ , \ f \ , \ g \ , \ h \ , \ j \ , \ k \ , \ l \ , \ m \ , \ n \ , \ p \ , \ q \ , \ r \ , \ s \ , \ t \ , \ v \ , \ w \ , \ x \ , \ z \ \} $$

Per indicare che un elemento appartiene all'insieme devi usare il simbolo di appartenenza ∈

Ad esempio, l'elemento a appartiene all'insieme A $$ a \in A $$

Se un elemento non appartiene all'insieme, invece, usa il simbolo di non appartenenza ∉

Ad esempio, l'elemento b appartiene all'insieme A $$ b \notin A $$

Quali sono i tipi di insiemi?

Ci sono due tipi principali di insiemi:

• Insiemi finiti
  Un insieme finito ha un numero definito di elementi. Ad esempio, l'insieme delle lettere dell'alfabeto inglese è un insieme finito perché è composto da 26 lettere. $$ A = \{ \ a \ , \ b \ , \ c \ , \ d \ , \ e \ , \ f \ , \ g \ , \ h \ , \ i \ , \ j \ , \ k \ , \ l \ , \ m \ , \ n \ , \ o \ , \\ \ \ \ \ \ \ \ \ \ \ \ p \ , \ q \ , \ r \ , \ s \ , \ t \ , \ u \ , \ v \ , \ w \ , \ x \ ,  \ y \ , \ z \ \} $$
• Insiemi infiniti
  Un insieme infinito ha un numero infinito di elementi. Ad esempio, l'insieme dei numeri interi positivi $ \mathbb{Z} $ è un insieme infinito.

Se un insieme \( A \) è composto da un numero finito di elementi, il totale di questi si chiama cardinalità dell'insieme ed è rappresentato dal simbolo \( |A| \).

Per esempio, considerando l'insieme \( V = \{ a, e, i, o, u \} \) delle vocali dell'alfabeto, esso contiene cinque elementi, quindi la cardinalità è \( |V| = 5 \). L'insieme delle lettere dell'alfabeto inglese ha, invece, una cardinalità \( |A| = 26 \) perché è composto da ventisei elementi.

Un esempio pratico

L'insieme A è l'insieme delle città europee e B è l'insieme delle città italiane.

$$ A = \{ \ Parigi \ , \ Roma \ , \ Berlino \ , \ Londra \ , \ ... \} $$

$$ B = \{ \ Roma \ , \ Milano \ , \ Firenze \ , \ Napoli \ , \ ... \} $$

Indica con la lettera a la città Roma.

$$ a \ = \ Roma $$

L'elemento a (Roma) appartiene sia all'insieme A (città europee) che all'insieme B (città italiane)

$$ a \in A $$

$$ a \in B $$

Ora indica con la lettera b la città Parigi.

$$ b \ = \ Parigi $$

L'elemento b (Parigi) appartiene all'insieme A (città europee) ma non appartiene all'insieme B (città italiane).

$$ b \in A $$

$$ b \notin B $$

A questo punto indica con la lettera c la città New York.

$$ c \ = \ New \ York $$

L'elemento c non appartiene né all'insieme A (città europee), né all'insieme B (città italiane)

$$ c \notin A $$

$$ c \notin B $$

Ora dovresti avere un'idea chiara di cos'è un insieme.