Il numero dei lati di un grafo
Il numero di spigoli (o lati) che un grafo semplice può avere dipende dal numero \( n \) di vertici .
Nel caso peggiore un grafo senza cicli ha \( n - 1 \) lati.
Nel caso con più spigoli, un grafo completo ha \( \frac{1}{2}n(n - 1) \) lati.
Dove un grafo è detto "semplice" se non ha anelli, spigoli che collegano un vertice a sé stesso, né spigoli duplicati tra due vertici. E' detto "connesso" se c'è un percorso tra ogni coppia di vertici. E' detto "completo" se ogni vertice è direttamente connesso a ogni altro vertice.
Qualsiasi grafo semplice con \( n \) vertici e più di \( \frac{1}{2}(n - 1)(n - 2) \) spigoli è connesso. Questo significa che se un grafo che c'è un percorso tra ogni coppia di vertici del grafo.
Il numero dei lati di un grafo dipende anche dal numero \( k \) componenti,
Un componente di un grafo è una sottosezione del grafo in cui ogni coppia di vertici è connessa tramite un percorso e non ci sono connessioni tra vertici di componenti diversi.
In altre parole, un componente è un "pezzo" del grafo dove puoi viaggiare da qualsiasi vertice a qualsiasi altro vertice all'interno di quel pezzo senza uscire dal componente.
Il numero di spigoli \( m \) di un grafo \( G \) con \( n \) vertici che ha \( k \) componenti è $$ n - k \le m \le \frac{1}{2}(n - k)(n - k + 1) $$
Quindi, un grafo con \( k \) componenti non ha meno di \( n - k \) lati e non ha più di \( \frac{1}{2}(n - k)(n - k + 1) \) lati.
Certo, facciamo un esempio pratico per chiarire il teorema.
Esempio
Consideriamo un grafo semplice con \( n = 6 \) vertici e \( k = 2 \) componenti.
Il numero minimo dei lati che può avere è \( n - k \)
$$ 6 - 2 = 4 $$
Quindi, il grafo deve avere almeno 4 spigoli.
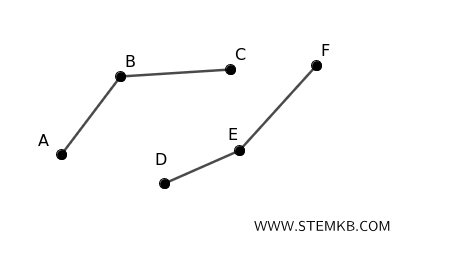
Immaginiamo due componenti. Il primo componente ha 3 vertici (A, B, C) e il secondo componente ha 3 vertici (D, E, F). Ogni componente è un albero (grafo connesso senza cicli) con 3 vertici, quindi ciascuno avrà \( 3 - 1 = 2 \) spigoli. In totale il grafo ha \( 2 + 2 = 4 \) lati.
Il numero massimo di lati che può avere è \( \frac{1}{2}(n - k)(n - k + 1) \)
$$ \frac{1}{2}(6 - 2)(6 - 2 + 1) = \frac{1}{2} \times 4 \times 5 = 10 $$
Quindi, il grafo può avere al massimo 10 spigoli.
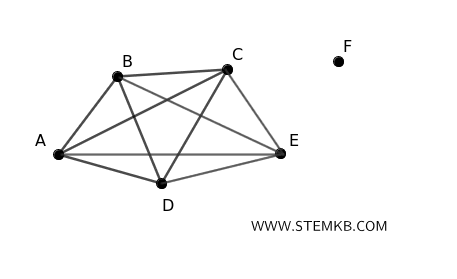
Immaginiamo di avere un grafo con $ n = 6 $ vertici, un componente (A, B, C, D, E) come un grafo completo con \( 5 \) vertici e un vertice F isolato. Il grafo completo su 5 vertici ha \( \frac{1}{2} \times 5 \times 4 = 10 \) spigoli. Il rimanente vertice F è isolato, quindi non aggiunge spigoli al grafo. In conclusione il grafo con $ n=6 $ vertici e $ k = 2 $ componenti può avere al massimo $ 10 $ spigoli.
Se un grafo con \( n = 6 \) vertici e ha più di \( \frac{1}{2}(n - 1)(n - 2) \) spigoli, allora è connesso.
$$ \frac{1}{2}(6 - 1)(6 - 2) = \frac{1}{2} \times 5 \times 4 = 10 $$
Quindi, un grafo con più di 10 spigoli è necessariamente connesso.
Per chiarire il concetto con un esempio, consideriamo un grafo con \( n = 6 \) vertici (A,B,C,D,E,F) e 11 spigoli per vedere che è connesso.
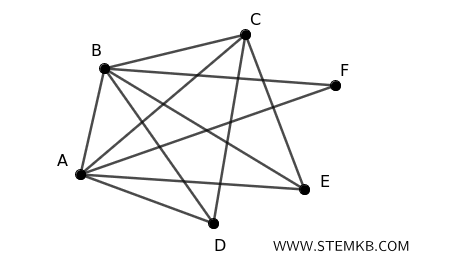
Il numero massimo di spigoli in un grafo completo con 6 vertici è: $$ \frac{1}{2} \times 6 \times (6 - 1) = \frac{1}{2} \times 6 \times 5 = 15 $$ Se un grafo con 6 vertici ha più di 10 spigoli, allora è connesso. $$ \frac{1}{2}(6 - 1)(6 - 2) = \frac{1}{2} \times 5 \times 4 = 10 $$ In questo caso il grafo ha 11 spigoli. Possiamo notare che ogni coppia di vertici è connessa, direttamente o indirettamente, attraverso una sequenza di spigoli. Quindi il grafo è connesso. Questo esempio conferma che se un grafo con \( n = 6 \) vertici ha più di 10 spigoli, esso è necessariamente connesso, come afferma il corollario.
Dimostrazione
Per dimostrare il limite inferiore di lati si usa l'induzione sul numero di spigoli. L'idea è che, rimuovendo un spigolo da un grafo che ha il minor numero possibile di spigoli, si aumenta il numero di componenti di 1.
Da questo, si dimostra che il numero di spigoli \( m \) deve essere almeno \( n - k \).
Per dimostrare il limite superiore di lati, invece, si considera il caso in cui ogni componente del grafo è un grafo completo (ogni vertice del componente è connesso a ogni altro vertice del componente).
L'obiettivo è dimostrare che il numero massimo di spigoli \( m \) in un grafo \( G \) con \( n \) vertici e \( k \) componenti è \( \frac{1}{2}(n - k)(n - k + 1) \).
Supponiamo di avere due componenti \( C_i \) e \( C_j \) con \( n_i \) e \( n_j \) vertici rispettivamente, dove \( n_i, n_j > 1 \). In altre parole, stiamo guardando due sottografi completi con più di un vertice ciascuno.
Ora sostituiamo \( C_i \) e \( C_j \) con nuovi grafi completi che hanno \( n_i + 1 \) e \( n_j - 1 \) vertici rispettivamente.
Facendo questo, il numero totale di vertici nel grafo \( G \) rimane invariato, ma cambia il numero di spigoli.
Il numero di spigoli di un grafo completo su \( n \) vertici è \( \frac{1}{2}n(n-1) \).
- Il numero di spigoli in \( C_i \) con \( n_i \) vertici è \( \frac{1}{2}n_i(n_i - 1) \).
- Il numero di spigoli in \( C_i \) dopo aver aggiunto un vertice (diventando \( n_i + 1 \)) è \( \frac{1}{2}(n_i + 1)n_i \).
La differenza nel numero di spigoli quando \( C_i \) passa da \( n_i \) a \( n_i + 1 \) è:
$$ \frac{1}{2}(n_i + 1)n_i - \frac{1}{2}n_i(n_i - 1) $$
$$ \frac{1}{2}[n_i^2 + n_i - n_i^2 + n_i] = \frac{1}{2}(2n_i) = n_i $$
Il numero di spigoli in \( C_j \) con \( n_j \) vertici è \( \frac{1}{2}n_j(n_j - 1) \).
Il numero di spigoli in \( C_j \) dopo aver rimosso un vertice (diventando \( n_j - 1 \)) è \( \frac{1}{2}(n_j - 1)(n_j - 2) \).
La differenza nel numero di spigoli quando \( C_j \) passa da \( n_j \) a \( n_j - 1 \) è:
$$ \frac{1}{2}n_j(n_j - 1) - \frac{1}{2}(n_j - 1)(n_j - 2) $$
$$ \frac{1}{2}[n_j^2 - n_j - n_j^2 + 2n_j - 1] = \frac{1}{2}(2n_j - 1) = n_j - 1 $$
Quindi, il cambiamento totale nel numero di spigoli quando sostituiamo i due componenti è:
$$ n_i - (n_j - 1) + 1 = n_i - n_j + 2 $$
Questo cambiamento è positivo, il che significa che aumentando il numero di vertici in uno dei componenti completi e diminuendolo nell'altro, aumenta il numero di spigoli.
Per massimizzare il numero di spigoli, ogni componente deve essere il più grande possibile, il che accade quando c'è un componente grande e gli altri sono isolati.
Se abbiamo \( k \) componenti, il componente più grande ha \( n - k + 1 \) vertici (un grafo completo), e gli altri \( k - 1 \) componenti sono singoli vertici isolati.
Il numero massimo di spigoli è quindi dato da:
$$ \frac{1}{2}(n - k + 1)(n - k) $$
Da qui segue il teorema:
$$ m \le \frac{1}{2}(n - k)(n - k + 1) $$
Se hai altre domande o se c'è qualcosa di specifico che non ti è chiaro, fammi sapere!

