La disuguaglianza tra la connettività dei vertici, degli spigoli e il grado minimo di un grafo

La connettività dei vertici $ \kappa(G) $ di un grafo non supera mai la connettività degli spigoli $ \lambda(G) $, la quale, a sua volta, è limitata dal grado minimo dei vertici $\delta(G) $. $$ \kappa(G) \leq \lambda(G) \leq \delta(G) $$

È una relazione fondamentale nella teoria dei grafi e riflette il fatto che:

La connettività dei vertici ($ \kappa(G) $) è sempre minore o uguale alla connettività degli spigoli ($ \lambda(G) $), poiché disconnettere un grafo tramite vertici è, in genere, più "costoso" rispetto alla rimozione di spigoli.
La connettività degli spigoli ($ \lambda(G) $) è, a sua volta, limitata dal grado minimo ($ \delta(G) $), poiché il vertice con il grado più basso stabilisce un limite massimo su quanto si possa mantenere la connettività solo con spigoli.

Questa disuguaglianza è un concetto di base ed è molto utile per analizzare la robustezza o la vulnerabilità strutturale di un grafo.

Un esempio pratico

Facciamo un esempio concreto utilizzando un grafo semplice per chiarire la disuguaglianza.

Immagina un grafo $ G $ con cinque vertici $ A $, $ B $, $ C $, $ D $ e $ E $, e sei: $(A, B) $ , $ (A, C) $, $ (B, C) $ , $ (B, D) $ , $ (B, E)$ , $ (D, E)$.

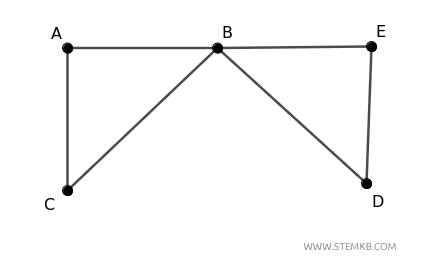
esempio di grafo

La connettività dei vertici $ \kappa(G) $ del grafo è il numero minimo di vertici che devi rimuovere per rendere il grafo disconnesso.

In questo caso, se rimuovi il vertice $ B $ ottieni due componenti disconnesse.

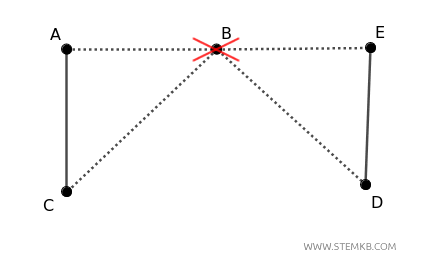
la connettività del grafo rispetto ai vertici

Quindi, la connettività dei vertici $ \kappa(G) = 1 $ perché basta rimuovere un solo vertice (o $ B $ o $ C $) per disconnettere il grafo.

$$ \kappa(G) = 1 $$

La connettività degli spigoli $ \lambda(G) $ è il numero minimo di spigoli che devi rimuovere per rendere il grafo disconnesso.

In questo caso, se rimuovi gli spigoli $(A, B)$ e $(B, C)$, il grafo si disconnette in due componenti: una che contiene i vertici $ A $ e $ C $, e l'altra che contiene $ B $ , $ D $ e $ E $.

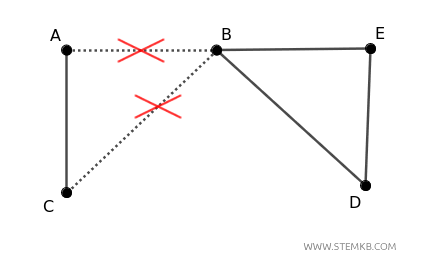
esempio

Quindi, la connettività degli spigoli è $ \lambda(G) = 2 $ perché occorre rimuovere almeno due spigoli per disconnettere il grafo.

$$ \lambda(G) = 2 $$

Il minimo grado $ \delta(G) $ è il grado minimo tra tutti i vertici del grafo.

In questo caso, i gradi dei vertici sono:

$ \deg(A) = 2 $ (connesso a $ B $ e $ C $),
$ \deg(B) = 4 $ (connesso a $ A $, $ C $ , $ D $, $ E $),
$ \deg(C) = 2 $ (connesso a $ A $, $ B $ ),
$ \deg(D) = 2 $ (connesso a $ B $ e $ E $).
$ \deg(E) = 2 $ (connesso a $ B $ e $ D $).

Quindi, il grado minimo dei vertici del grafo è $ \delta(G) = 2 $.

$$ \delta(G) = 2 $$

Riepilogando abbiamo trovato che $ \kappa(G) = 1 $, $ \lambda(G) = 2 $ e $ \delta(G) = 2 $

Quindi, la disuguaglianza $ \kappa(G) \leq \lambda(G) \leq \delta(G) $ è verificata:

$$ 1 \leq 2 \leq 2 $$

Questo esempio mostra che per disconnettere il grafo è sufficiente rimuovere un vertice (la connettività dei vertici è 1).

Tuttavia, per disconnettere il grafo tramite spigoli, occorre rimuoverne almeno due (la connettività degli spigoli è 2).

Il vertice con il minor numero di connessioni nel grafo ha grado 2, che rappresenta un limite superiore naturale per la connettività degli spigoli.