Insieme separatore di vertici

Un insieme separatore di vertici è un insieme di nodi (vertici) in un grafo che, se rimosso, rende il grafo disconnesso.

In altre parole, eliminando questi vertici e i loro archi associati, il grafo viene diviso in due o più sottografi che non sono più collegati tra loro.

E' chiamato anche "insieme separante di vertici" o semplicemente "insieme separatore".

Un concetto speciale che rientra in questo contesto è il vertice di taglio (o cut-vertex). Si tratta di un particolare vertice che, se rimosso, disconnette il grafo. È l'esempio più semplice di un insieme separatore, dove l'insieme contiene un solo vertice.

La connettività di un grafo, indicata con \( \kappa(G) \), è il numero minimo di vertici che devono essere rimossi per disconnettere il grafo. Quindi, l'insieme separatore più piccolo è proprio quello che definisce la connettività del grafo.

Esempio

Considera un grafo connesso con tre vertici \( A \), \( B \) e \( C \), dove \( A \) è collegato a \( B \), \( B \) è collegato a \( C \).

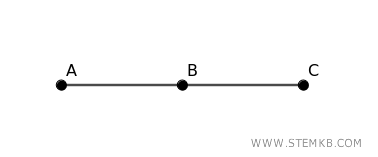
Se rimuovi il nodo \( B \), il grafo si disconnette, lasciando \( A \) e \( C \) senza un collegamento. In questo caso, \( B \) è un vertice di taglio.

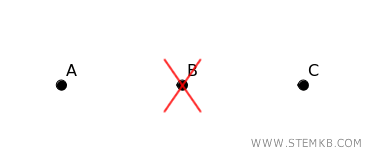
In questo caso il grafo ha connettività $ \kappa(G)=1 $ ovvero è 1-connesso, perché basta rimuovere un vertice per disconnetterlo.

Esempio 2

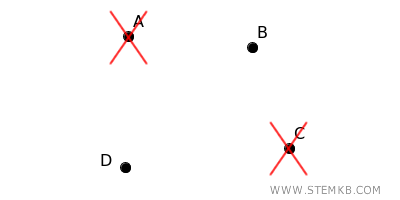
Ora considera un grafo connesso con quattro vertici \( A \), \( B \), \( C \) e \( D \),  con gli archi \( (A, B) \), \( (B, C) \), \( (C, D) \), e \( (D, A) \) che formano un quadrilatero.

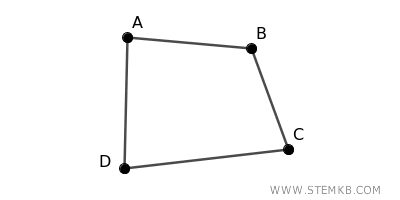
In questo caso, la rimozione di un singolo vertice non è sufficiente a disconnettere il grafo, perché gli altri tre vertici rimangono comunque collegati.

Per esempio, se rimuovi il vertice \( A \), rimangono ancora i collegamenti tra \( B, C, \) e \( D \) tramite gli archi \( (B, C) \) e \( (C, D) \).

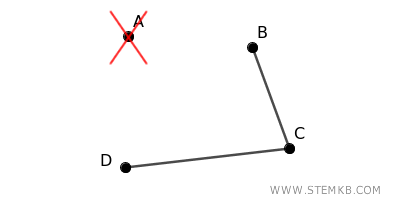
Devi rimuovere almeno due vertici, come \( A \) e \( C \) o \( B \) e \( D \), per separare completamente il grafo in due parti disconnesse.

Pertanto, questo grafo è 2-connesso, con connettività \( \kappa(G) = 2 \), poiché è necessario rimuovere almeno due vertici per renderlo disconnesso.

Teorema di Menger

Un importante risultato teorico associato agli insiemi separatori è il Teorema di Menger. Questo teorema stabilisce che:

La connettività di un grafo (cioè il numero minimo di vertici da rimuovere per separare il grafo) è uguale al numero massimo di percorsi disgiunti tra due vertici qualsiasi del grafo.

Ad esempio, immagina di avere due vertici \( A \) e \( B \) in un grafo.

Esistono due percorsi distinti tra \( A \) e \( B \) che non condividono vertici (eccetto \( A \) e \( B \)).

1. $ A \rightarrow B $
2. $ A \rightarrow D \rightarrow C \rightarrow B $

Quindi, la connettività del grafo è almeno 2.

Le applicazioni degli insiemi separatori

Gli insiemi separatori di vertici sono strumenti fondamentali nella teoria dei grafi, essenziali per comprendere la robustezza e la vulnerabilità delle reti.

Analizzando come un grafo può essere disconnesso rimuovendo uno o più vertici, puoi fare previsioni su come mantenere una rete connessa o su quali siano i punti critici da rinforzare.

Gli insiemi separatori sono utilizzati per identificare i punti critici della rete, la cui rimozione disconnetterebbe il sistema.

Esempio. Sono particolarmente utili per progettare reti di comunicazione, dove i vertici potrebbero rappresentare i server, e i collegamenti potrebbero essere le connessioni tra i server, oppure sistemi di trasporto. Negli studi di sicurezza delle reti informatiche o energetiche, gli insiemi separatori individuano i componenti critici da proteggere per evitare che l'intero sistema collassi in caso di attacchi o guasti.