Grafo planare
Un grafo planare è un tipo di grafo che può essere disegnato su un piano senza che le sue linee, o archi, si intersechino, ad eccezione dei loro punti terminali, ovvero i vertici.
Ciò significa che è possibile disporre i vertici e gli archi di un grafo planare in modo che nessun arco si sovrapponga a un altro.
Per ogni grafo planare connesso e finito, vale la relazione di Eulero
$$ V−E+F=2 $$
Dove V è il numero di vertici, E è il numero di archi, e F è il numero di facce, ovvero le regioni di spazio racchiuse dagli spigoli contando anche la regione esterna al grafo.
Questa formula è molto utile per dimostrare se un dato grafo è planare o meno.
Esempio
Questo è un grafo planare composto da 5 vertici e 7 spigoli.
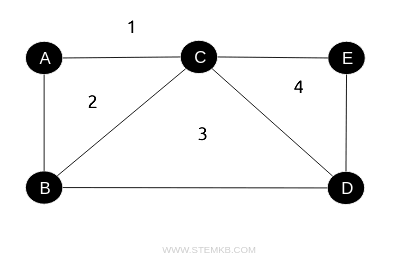
Il grafo è composto da F=4 facce di cui 3 regioni interne e una regione esterna.
$$ V−E+F=2 $$
$$ 5−7+4=2 $$
$$ 2 = 2 $$
La relazione tra vertici, spigoli e facce di Eulero è soddisfatta. Quindi si tratta di un grafo planare.
Esempio 2
Questo grafo è simile al precedente ma non è un grafo planare perché due spigoli, AD e BC, si intersecano.
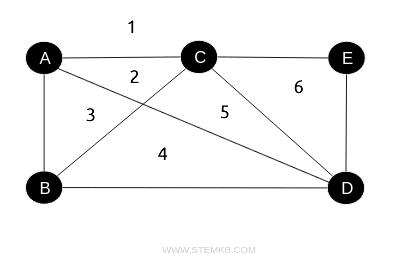
In questo caso la formula di Eulero non viene confermata, perché ci sono V=5 vertici, E=8 spigoli e F=6 facce.
$$ V−E+F=2 $$
$$ 5−8+6=2 $$
$$ 3 \ne 2 $$

