Isomorfismo dei grafi
Un isomorfismo tra due grafi \( G \) e \( H \) è una biiezione tra i vertici di \( G \) e \( H \) che preserva le connessioni tra i vertici. $$ G \cong H $$
In altre parole, due grafi isomorfi sono lo stesso grafo dal punto di vista della teoria dei grafi, anche se possono apparire diversi a prima vista.
Un isomorfismo tra due grafi permette di "mappare" i vertici di un grafo sui vertici dell'altro in modo tale che le strutture dei due grafi siano identiche.
Formalmente, un isomorfismo tra due grafi \( G = (V_G, E_G) \) e \( H = (V_H, E_H) \) è una funzione biiettiva
$$ f: V_G \to V_H $$
tale che per ogni \( u, v \in V_G \):
$$ \{u, v\} \in E_G \iff \{f(u), f(v)\} \in E_H $$
Ciò significa che esiste un'arco tra due vertici \( u \) e \( v \) in \( G \) se e solo se esiste un arco tra i vertici \( f(u) \) e \( f(v) \) in \( H \).
Gli isomorfismi sono importanti perché ci permettono di riconoscere quando due grafi sono "essenzialmente lo stesso". Due grafi appartengono alla stessa classe di isomorfismo se esiste un isomorfismo tra di essi. Quindi, una classe di isomorfismo è un gruppo di grafi che sono tutti isomorfi tra loro. Quindi,
Esempio
Consideriamo due semplici grafi \( G \) e \( H \):
Grafo \( G \)
Il grafo G ha tre vertici \( V_G = \{1, 2, 3\} \) e due archi \( E_G = \{\{1, 2\}, \{2, 3\}\} \)
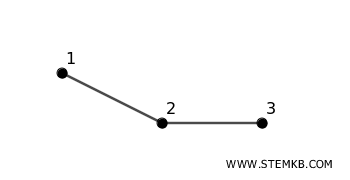
Grafo \( H \)
Il grafo H ha tre vertici: \( V_H = \{A, B, C\} \) e due archi: \( E_H = \{\{A, B\}, \{B, C\}\} \)
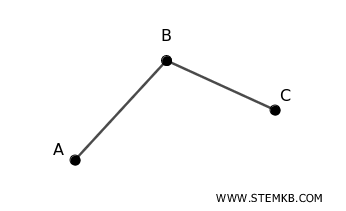
Un possibile isomorfismo \( f \) tra \( G \) e \( H \) può essere definito come segue:
$$ f(1) = A $$
$$ f(2) = B $$
$$ f(3) = C $$
Verifichiamo che \( f \) sia un isomorfismo:
\( \{1, 2\} \in E_G \rightarrow \{f(1), f(2)\} = \{A, B\} \in E_H \)
\( \{2, 3\} \in E_G \rightarrow \{f(2), f(3)\} = \{B, C\} \in E_H \)
Quindi, la funzione \( f \) preserva le connessioni tra i vertici e \( f \) è un isomorfismo tra \( G \) e \( H \).
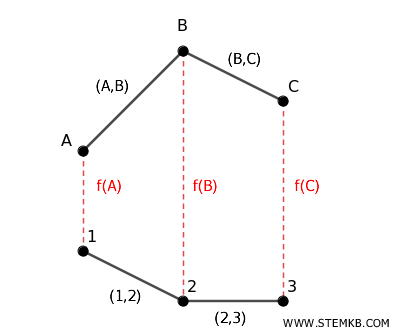
In conclusione, i grafi G e H sono isomorfi, quindi appartengono alla stessa classe di isomorfismo.
Come verificare se due grafi sono isomorfi
Uno dei metodi per verificare se due grafi sono isomorfi è rietichettare i vertici e confrontare le loro matrici di adiacenza.
Ecco la procedura per verificarel'Isomorfismo
- Costruzione delle matrici di adiacenza
Costruisci le matrici di adiacenza \( A_G \) e \( A_H \) per i grafi \( G \) e \( H \). - Rietichettatura dei vertici
Considera tutte le possibili permutazioni dei vertici di uno dei grafi, ad esempio \( G \). - Permutazione delle matrici
Per ogni permutazione, rietichetta i vertici di \( G \) e costruisci la matrice di adiacenza corrispondente. - Confronto delle matrici
Confronta la matrice di adiacenza rietichettata di \( G \) con la matrice di adiacenza di \( H \). Se trovi una permutazione per cui le matrici sono identiche, i grafi sono isomorfi.
Facciamo un esempio pratico
Consideriamo due grafi \( G \) e \( H \):
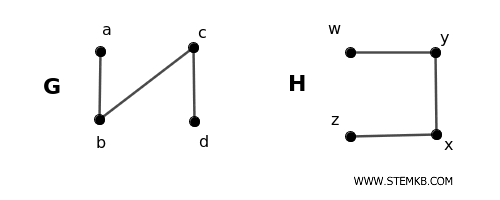
Il Il grafo G ha quattro vertici \( V_G = \{a, b, c, d\} \) e tre archi \( E_G = \{\{a, b\}, \{b, c\}, \{c, d\} \} \)
Il grafo H ha quattro vertici \( V_H = \{w, x, y, z \} \) e tre archi \( E_H = \{\{w, x\}, \{x, y\}, \{y, z\} \} \)
Le matrici di adiacenza per \( G \) e \( H \) sono rispettivamente:
\[ A_G =
\begin{array}{c|cccc}
& a & b & c & d \\
\hline
a & 0 & 1 & 0 & 0 \\
b & 1 & 0 & 1 & 0 \\
c & 0 & 1 & 0 & 1 \\
d & 0 & 0 & 1 & 0 \\
\end{array}
\]
\[ A_H =
\begin{array}{c|cccc}
& w & y & x & y \\
\hline
w & 0 & 0 & 0 & 1 \\
y & 0 & 0 & 1 & 1 \\
x & 0 & 1 & 0 & 0 \\
y & 1 & 1 & 0 & 0 \\
\end{array}
\]
Ora proviamo qualche permutazione sulle righe e le colonne sulla matrice $ A_G $ per renderla uguale alla matrice $ A_H $
Ad esempio, spostiamo la seconda riga/colonna alla terza riga/colonna ($ b \leftrightarrow c $).
\[ A_G =\begin{array}{c|cccc}
& a & c & b & d \\
\hline
a & 0 & 0 & 1 & 0 \\
c & 0 & 0 & 1 & 1 \\
b & 1 & 1 & 0 & 0 \\
d & 0 & 1 & 0 & 0 \\
\end{array}
\]
Poi scambiamo la terza riga/colonna con la quarta riga/colonna ($ b \leftrightarrow d $)
\[ A_G =\begin{array}{c|cccc}
& a & c & d & b \\
\hline
a & 0 & 0 & 0 & 1 \\
c & 0 & 0 & 1 & 1 \\
d & 0 & 1 & 0 & 0 \\
b & 1 & 1 & 0 & 0 \\
\end{array}
\]
Ora la matrice di adiacenza $ A_G $ è uguale alla matrice $ A_H $
\[ A_G =\begin{array}{c|cccc}
& a & c & b & d \\
\hline
a & 0 & 0 & 0 & 1 \\
c & 0 & 0 & 1 & 1 \\
d & 0 & 1 & 0 & 0 \\
b & 1 & 1 & 0 & 0 \\
\end{array} = A_H = \begin{array}{c|cccc}
& w & y & x & y \\
\hline
w & 0 & 0 & 0 & 1 \\
y & 0 & 0 & 1 & 1 \\
x & 0 & 1 & 0 & 0 \\
y & 1 & 1 & 0 & 0 \\
\end{array}
\]
Questo vuole dire che i grafi $ G $ e $ H $ sono grafi isomorfi.
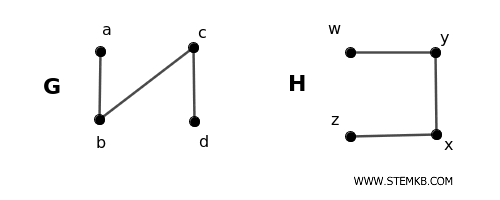
In altre parole, se consideriamo la permutazione \( (a \rightarrow w, b \rightarrow y, c \rightarrow x, d \rightarrow z ) \) vediamo che \( A_G \) e \( A_H \) sono identici.
Questo metodo è teoricamente corretto ma può essere computazionalmente costoso, poiché il numero di permutazioni da considerare cresce fattorialmente con il numero di vertici (\( n! \)). Dove n! è il fattoriale di n.
Ad esempio, per un grafo con n=4 vertici ci sono 4!=24 permutazioni
$$ 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 $$
Ma già per un grafo con n=5 vertici ci sono ben 5!=120 permutazioni.
$$ 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 $$
E la situazione peggiora per i grafi più grandi.
Il confronto delle matrici di adiacenza tramite rietichettatura dei vertici è un metodo valido per verificare l'isomorfismo tra due grafi. Sebbene possa essere inefficiente per grafi di grandi dimensioni, è utile per comprendere il concetto e applicabile a grafi più piccoli. In alternativa, esistono algoritmi più efficienti per verificare l'isomorfismo tra grafi, come l'algoritmo di Weisfeiler-Lehman.
Le proprietà dei grafi isomorfi
Quando due grafi sono isomorfi, le loro proprietà strutturali fondamentali sono preservate
Questo è essenziale perché l'isomorfismo implica che i grafi, sebbene possano apparire diversi, sono in realtà identici nella loro struttura intrinseca.
Vediamo in dettaglio alcune di queste proprietà .
- Numero di vertici e archi
Due grafi isomorfi hanno lo stesso numero di vertici e lo stesso numero di archi. Questo è una conseguenza diretta della definizione di isomorfismo che richiede una corrispondenza biiettiva tra i vertici che preserva le connessioni (archi). - Grado dei vertici
In due grafi isomorfi, ogni vertice ha lo stesso grado (numero di archi incidenti). Se un vertice \( v \) in \( G \) ha grado \( k \), il vertice corrispondente \( f(v) \) in \( H \) avrà anche esso grado \( k \). - Sottografi
Qualsiasi sottografo di un grafo isomorfo corrisponde a un sottografo dell'altro grafo che è anch'esso isomorfo. In altre parole, le proprietà dei sottografi sono preservate. - Ciclo e cammini
I cicli (sequenze chiuse di vertici connessi) e i cammini (sequenze aperte di vertici connessi) in un grafo hanno corrispondenze esatte nell'altro grafo. Se esiste un ciclo di lunghezza \( k \) in \( G \), esisterà un ciclo di lunghezza \( k \) in \( H \). - Connettività
La connettività di un grafo è preservata sotto l'isomorfismo. Se \( G \) è connesso (cioè c'è un cammino tra ogni coppia di vertici), allora \( H \) sarà connesso. - Complemento del grafo
I complementi di due grafi isomorfi sono anch'essi isomorfi. Il complemento di un grafo \( G \) è un grafo in cui due vertici sono connessi se e solo se non sono connessi in \( G \).
La relazione di isomorfismo è una relazione di equivalenza
Per capire meglio, analizziamo le tre proprietà principali delle relazioni di equivalenza: riflessività, simmetria e transitività, nel contesto dei grafi isomorfi.
- Riflessiva
Ogni grafo G è isomorfo a se stesso. Questo è vero perché l'identità dei vertici e degli archi di G può essere considerata come un isomorfismo. - Simmetrica
Se un grafo G è isomorfo a un grafo H (G≅H), allora H è isomorfo a G (H≅G). - Transitiva
Se un grafo G è isomorfo a un grafo H (G≅H), e H è isomorfo a un grafo F (H≅F), allora G è isomorfo a F (G≅F).
Quindi, i grafi isomorfi formano classi di equivalenza, dove ogni classe contiene tutti i grafi che sono isomorfi tra loro.

