Insieme di disconnessione di un grafo
Un insieme di disconnessione in un grafo connesso \( G \) è un insieme di spigoli la cui eliminazione aumenta il numero di componenti del grafo, cioè rende il grafo disconnesso.
In altre parole, un insieme di disconnessione è un gruppo di spigoli che, se rimosso, fa sì che il grafo connesso si divida in parti separate tra loro.
E' uno dei concetti chiave nello studio della connettività dei grafi.
L'identificazione degli insiemi di disconnessione è cruciale in vari ambiti applicativi. Ad esempio, in uan rete di telecomunicazioni o di trasporto permette di individuare i punti critici o deboli della rete e, quindi, le possibili vulnerabilità.
Esempio
Consideriamo un grafo connesso \( G \) formato da cinque vertici (A, B, C, D, E) e sette spigoli (A-B), (A-C), (A-D), (B-C), (C-D), (C-E), (D-E).
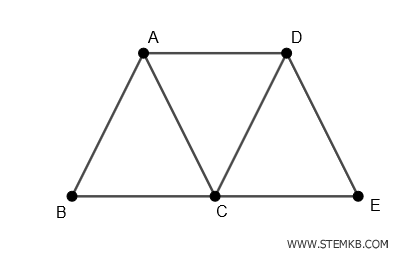
Questo grafo è connesso perché esiste un percorso tra qualsiasi coppia di vertici.
Ora, identifichiamo un insieme di disconnessione composto dai seguenti spigoli:
$$ \{(A-B), (B-C) \} $$
Se rimuoviamo questi spigoli, otteniamo due componenti separati:
- Il primo componente è composto dal solo vertice B
- Il secondo componente è composto dai vertici A, C, D, E
Quindi, rimuovendo gli spigoli (A-B) e (B-C), il grafo inizialmente connesso diventa disconnesso.
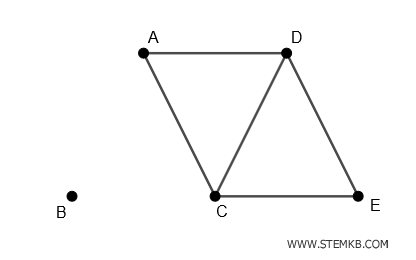
Se i vertici del grafo rappresentassero città e gli spigoli le linee ferroviarie, ciò significherebbe che la città B rimarrebbe isolata nel caso di un guasto simultaneo alle linee (A-B) e (A-C). Questo esempio illustra l'importanza pratica degli insiemi di disconnessione.
Un grafo può avere anche più di un insieme di disconnessione.
Ad esempio, nel grafo G un altro insieme di disconnessione è l'insieme di spigoli:
$$ \{(A-D), (D-C), (C-E) \} $$
Anche in questo caso se eliminiamo questi spigoli otteniamo un grafo disconnesso composto da due componenti:
La prima componente è composta dai vertici A, B, C mentre la seconda dai vertici D, E.
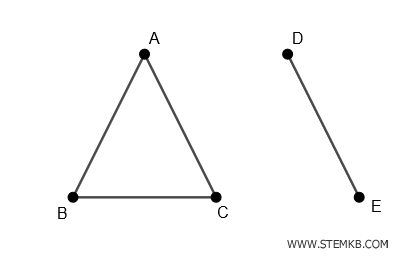
Riepilogando, un grafo può avere molti insiemi di disconnessione.
L'insieme di disconnessione che rimuove il minore numero di spigoli in un grafo è detto taglio.

