
Digrafo connesso e fortemente connesso
Un digrafo è connesso se, ignorando la direzione degli archi, esiste un percorso tra ogni coppia di nodi. È fortemente connesso se, seguendo la direzione degli archi, è possibile raggiungere ogni nodo partendo da qualsiasi altro nodo.
Vediamo di approfondire questa differenza facendo qualche esempio pratico.
Un digrafo (cioè un grafo diretto) è "connesso" se esiste un percorso tra qualsiasi coppia di vertici, ma solo se ignori le direzioni degli archi.
Questo significa che, considerando il grafo come se fosse non diretto, quindi trascurando il verso degli archi, puoi sempre raggiungere un vertice partendo da qualsiasi altro.
Ecco un esempio pratico basato su un digrafo con 5 nodi A, B, C, D, E e 5 archi (A,B), (B,C), (C,D), (D,A), (E,D).
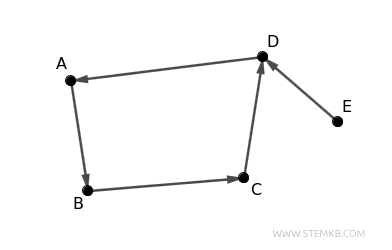
Questo grafo è connesso perché eliminando il verso da ogni arco, puoi raggiungere ogni nodo da qualsiasi altro nodo.
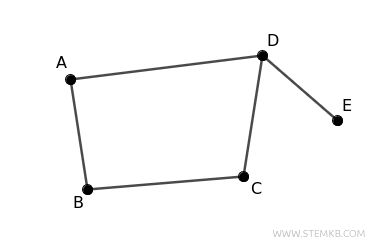
D'altra parte, in un digrafo "fortemente connesso" non è sufficiente ignorare le direzioni: deve essere possibile raggiungere ogni vertice partendo da qualunque altro seguendo sempre la direzione degli archi.
Questo requisito è più restrittivo, perché implica che ci siano percorsi diretti tra ogni coppia di vertici.
Ecco un esempio pratico basato su un digrafo con 5 nodi A, B, C, D, E e 5 archi (A,B), (B,C), (C,D), (D,A), (E,D). Questo grafo è connesso ma non è fortemente connesso, perché ad esempio il nodo E non è raggiungibile dal nodo D.

In questo caso è necessario tenere conto della direzione degli archi. Per rendere il digrafo fortemente connesso, è sufficiente aggiungere almeno un arco che colleghi il nodo \(E\) a un qualsiasi altro nodo già presente nel grafo. Ad esempio, aggiungendo un arco da \(C\) a \(E\) (ovvero \(C \to E\)), il digrafo diventa fortemente connesso, poiché ora esiste un percorso diretto tra ogni coppia di nodi e ciascun nodo raggiungibile da qualsiasi altro.
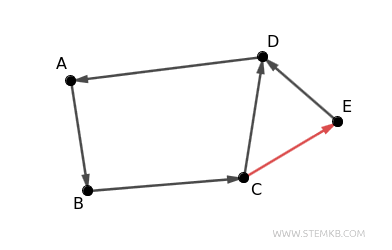
Va da sé che ogni digrafo fortemente connesso è dunque anche connesso, ma non vale il viceversa.
Questa distinzione è essenziale in molti problemi pratici, come la pianificazione dei sistemi di trasporto o di comunicazione, in cui è importante capire se il collegamento tra nodi rimane anche quando si seguono solo i percorsi "nella direzione giusta".

