Grafo connesso
Un grafo connesso è un tipo di grafo in cui esiste un cammino tra ogni coppia di vertici.
In altre parole, partendo da qualsiasi vertice, è possibile raggiungere qualsiasi altro vertice attraverso una serie di archi del grafo.
Questo tipo di grafo non presenta vertici o gruppi di vertici isolati, il che significa che tutti i vertici sono in qualche modo collegati tra loro.
Questa proprietà di connessione è particolarmente importante in molte applicazioni pratiche dei grafi, come nella progettazione di reti di telecomunicazione, nella pianificazione urbana per la costruzione di strade, o nella teoria dei circuiti elettrici, dove ogni componente deve essere accessibile.
La connessione può essere rilevata sia nei grafi non orientati (grafi semplici) sia in quelli orientati (digrafi).
La connessione nei grafi semplici
In termini più formali, un grafo non orientato è definito connesso se per ogni coppia di vertici \( u \) e \( v \) esiste un cammino che li collega.
La connessione nei digrafi
Se il grafo è orientato, è definito connesso se per ogni coppia di vertici \( u \) e \( v \) esistono cammini in entrambe le direzioni, da \( u \) a \( v \) e da \( v \) a \( u \).
Esempio
Consideriamo un semplice esempio di grafo connesso usando cinque vertici numerati da 1 a 5.
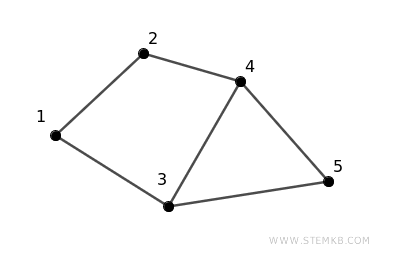
Le connessioni (o archi) tra i vertici sono così configurate:
- Il vertice 1 è connesso al vertice 2 e al vertice 3.
- Il vertice 2 è collegato al vertice 4.
- Il vertice 3 è collegato al vertice 4 e al vertice 5.
- Il vertice 4 è collegato al vertice 5.
Questa configurazione forma un grafo connesso perché è possibile raggiungere ogni vertice partendo da qualsiasi altro vertice attraverso una sequenza di archi.
Ad esempio, per andare dal vertice 1 al vertice 5, si può seguire il percorso: 1 -> 3 -> 5.
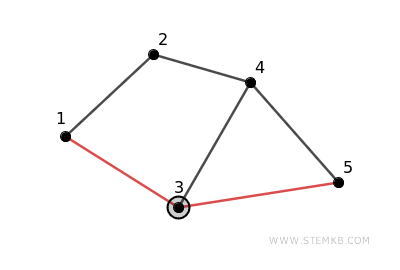
Questo tipo di struttura assicura che non ci siano vertici isolati e che ogni coppia di vertici sia collegata indirettamente o direttamente tramite altri vertici e archi.
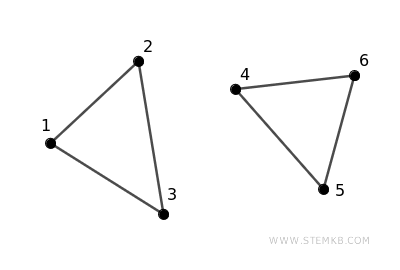
Esempio di grafo non connesso. Questo grafo non è connesso perché non tutti i vertici sono collegati direttamente o indirettamente tra loro. Ad esempio, non c'è un cammino che permette di spostarsi dal vertice 2 al vertice 4, né di andare dal vertice 1 al vertice 6, ecc.
Esempio di digrafo connesso
Ecco un esempio di digrafo fortemente connesso utilizzando cinque vertici, numerati da 1 a 5:
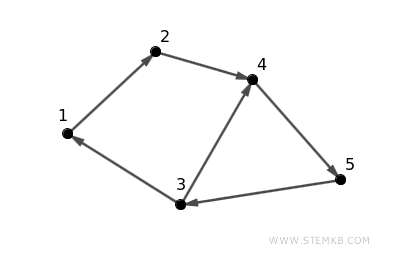
Le connessione dai nodi sono le seguenti:
- Dal vertice 1 esce un arco verso il vertice 2.
- Dal vertice 2 esce un arco verso il vertice 4.
- Dal vertice 3 esce un arco verso il vertice 1 e un arco verso il vertice 4.
- Dal vertice 4 esce un arco verso il vertice 5.
- Dal vertice 5 esce un arco verso il vertice 3.
Si tratta di un digrafo connesso perché ogni vertice è raggiungibile da ogni altro attraverso un percorso orientato.
Ad esempio, il percorso 1→2→4→5 connette il nodo 1 al nodo 5. Nel verso opposto, il percorso 5→3→1 collega il nodo 5 al nodo 1.
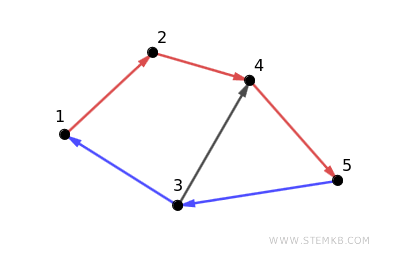
In questo particolare caso, il digrafo forma anche un ciclo che include tutti i vertici.
In altre parole, non solo è possibile raggiungere ogni vertice partendo da qualsiasi altro vertice, ma è anche possibile ritornare al vertice di partenza seguendo la sequenza degli archi.
Questo completa un ciclo che passa attraverso tutti i vertici, dimostrando la forte connessione nel digrafo.
Ad esempio, il percorso 1→2→4→5→3→1 forma un ciclo che passa per tutti i vertici, parte dal vertice 1 e ritorna al vertice 1.
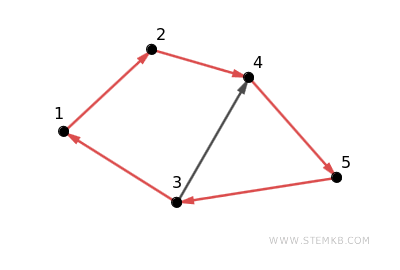
In particolar modo, in questo esempio il digrafo è fortemente connesso perché soddisfa la condizione che per ogni coppia di vertici u e v, esistono cammini orientati da u a v e da v a u.
Viceversa, un digrafo è detto debolmente connesso se, ignorando la direzione degli archi, esiste un cammino che collega ogni coppia di vertici.
In altre parole, se trasformiamo tutti gli archi direzionati in archi non direzionati (rendendoli bidirezionali) e il grafo risultante è connesso, allora il digrafo originale è debolmente connesso.
Ad esempio, questo digrafo non è fortemente connesso perché non è possibile spostarsi dal vertice 3 al vertice 4.
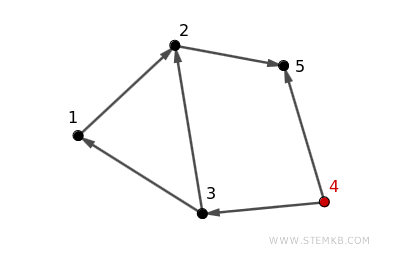
Tuttavia, considerando tutti gli archi come bidirezionali esiste un cammino che collega ogni vertice con qualsiasi altro vertice. Quindi, il digrafo è debolmente connesso.

