La connettività degli spigoli di un grafo
La connettività degli spigoli di un grafo è il numero minimo di spigoli che devono essere rimossi affinché un grafo connesso diventi disconnesso. E' indicata con $ λ(G) $
In altre parole, è il numero minimo di spigoli che devi eliminare affinché non esista più un percorso tra almeno una coppia di vertici del grafo, dividendo così il grafo in due o più componenti non connesse tra loro.
La connettività degli spigoli misura la resilienza di un grafo rispetto alla rimozione degli spigoli.
Indica quanti spigoli devono essere rimossi per rompere la connessione tra i vertici del grafo.
La connettività degli spigoli è importante in molti campi, come nelle reti di comunicazione, dove si vuole garantire che la rete rimanga connessa anche in caso di guasti ad alcune connessioni (spigoli). Un grafo con una connettività degli spigoli più alta è considerato più robusto rispetto a un grafo con una connettività degli spigoli più bassa, poiché può tollerare la rimozione di più spigoli prima di diventare disconnesso.
Un grafo si dice "k-edge-connected" se la sua connettività degli spigoli è almeno k, cioè se servono almeno k spigoli per disconnetterlo $ \lambda(G) \ge k $
Esempio
Considera un grafo costituito da un triangolo (tre vertici collegati da tre spigoli).
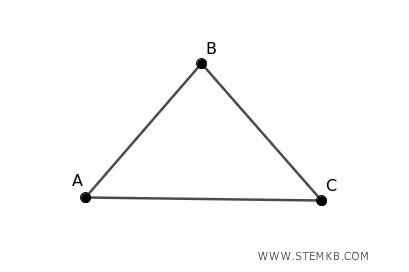
Si tratta di un grafo connesso perché esiste un percorso tra ogni coppia di vertici del grafo.
La connettività degli spigoli λ(G) di questo grafo è 2, perché bisogna rimuovere almeno due spigoli per disconnettere il grafo, cioè per fare in modo che almeno una coppia di vertici non sia più collegata da alcun percorso.
$$ λ(G) = 2 $$
Ad esempio, per disconnettere il grafo puoi eliminare gli spigoli (A,B) e (A,C) oppure gli spigoli (B,C) e (A,B).
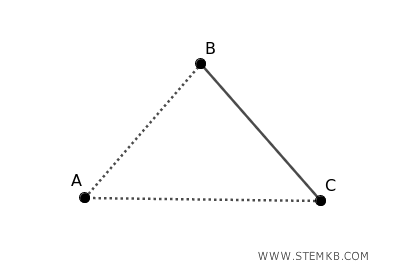
Quindi il grafo è 2-edge-connected, il che significa che devi rimuovere almeno due spigoli per disconnetterlo.
Questo vuole dire che il grafo è sia 1-edge-connected che 2-edge-connected, perché è necessario rimuovere almeno due spigoli per trasformarlo in un grafo disconnesso. Ma non è 3-edge-connected.
Teorema di Menger sulla connettività del grafo
Un grafo \( G \) è k-edge-connesso se e solo se qualsiasi coppia di insiemi distinti di vertici di \( G \) è collegata da almeno \( k \) cammini disgiunti per spigoli, ovvero cammini che non hanno spigoli in comune.
Questo teorema è stato formulato dal matematico austriaco Karl Menger, collega la connettività di un grafo con il numero di cammini disgiunti tra due insiemi di vertici.
Il teorema di Menger stabilisce una condizione equivalente per la k-edge-connettività, ovvero la proprietà di un grafo di rimanere connesso anche se si rimuovono fino a \( k-1 \) spigoli.
Essere k-edge-connesso significa che, per separare (o disconnettere) due insiemi di vertici, è necessario rimuovere almeno \( k \) spigoli.
Quindi, se due insiemi di vertici distinti sono collegati da almeno \( k \) cammini senza spigoli in comune, il grafo ha un certo livello di resistenza alle disconnessioni.
Un esempio pratico
Riprendiamo il grafo dell'esempio precedente con tre vertici \( A \), \( B \) e \( C \) e tre spigoli \((A, B)\), \((B, C)\) e \((A, C)\).

Vediamo come il teorema di Menger si applica qui per la k-edge-connettività.
In questo grafo, qualsiasi coppia di vertici è connessa da almeno due cammini disgiunti per spigoli. Ad esempio:
- Tra \( A \) e \( C \) esistono due cammini disgiunti per spigoli:
1. Il cammino diretto \((A, C)\),
2. Il cammino indiretto \((A, B) \rightarrow (B, C)\). - Tra \( A \) e \( B \) esistono anche due cammini disgiunti:
1. Il cammino diretto \((A, B)\),
2. Il cammino indiretto \((A, C) \rightarrow (C, B)\). - Tra \( B \) e \( C \) esistono due cammini disgiunti:
1. Il cammino diretto \((B, C)\)
2. Il cammino indiretto \((B, A) \rightarrow (A, C)\).
Poiché tra qualsiasi coppia di vertici distinti ci sono almeno due cammini disgiunti per spigoli, il grafo è 2-edge-connesso.
In altre parole, secondo il teorema di Menger, poiché tra ogni coppia di vertici ci sono due cammini senza spigoli in comune, è necessario rimuovere almeno due spigoli per disconnettere una coppia di vertici.
Se provassimo a rimuovere uno solo degli spigoli del grafo, i tre vertici sarebbero ancora tutti connessi.
Ad esempio, per disconnettere i vertici \( A \) e \( C \), devi rimuovere sia lo spigolo \((A, B)\) che \((B, C)\) oppure sia \((A, C)\) che un altro spigolo.
Pertanto, il teorema di Menger si verifica in questo grafo perché il grafo è 2-edge-connesso, ovvero soddisfa la proprietà che ogni coppia di vertici distinti è collegata da almeno due cammini disgiunti per spigoli.
Questo indica che il grafo ha una certa robustezza: la connessione tra i vertici non si perde finché non si rimuovono almeno due spigoli.
Il teorema di Menger fornisce una potente caratterizzazione della connettività in termini di cammini disgiunti.

