Cutset di un grafo connesso

Un cutset (o taglio) di un grafo connesso è un insieme di disconnessione minimo.

Dove un insieme di disconnessione è un insieme di spigoli in un grafo connesso la cui rimozione rende il grafo disconnesso.

Il cutset è il più piccolo insieme di disconnessione del grafo. Il che significa che nessun sottoinsieme proprio del cutset può essere un insieme di disconnessione.

In altre parole, se si rimuovesse anche un solo spigolo in meno rispetto all'intero cutset, il grafo resterebbe comunque connesso.

Questo vuol dire che ogni cutset è un insieme di disconnessione ma non tutti gli insiemi di disconnessione sono cutset.

La rimozione di tutti gli spigoli contenuti in un cutset deve necessariamente dividere il grafo in due o più componenti disconnessi.

E' un concetto fondamentale nella teoria dei grafi, strettamente legato alla connettività del grafo.

Esempio

Consideriamo un grafo composto da 6 vertici e 7 spigoli.

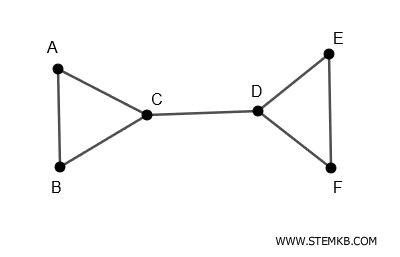
Supponiamo di voler trovare un cutset che, se rimosso, disconnette il grafo.

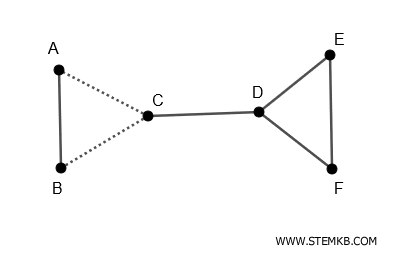
Se rimuoviamo gli spigoli \((A-B)\) e \((B-C)\), il grafo si disconnette in due componenti.

Quindi l'insieme $ \{ (A-B), (B-C)  \} $ è un insieme di disconnessione del grafo.

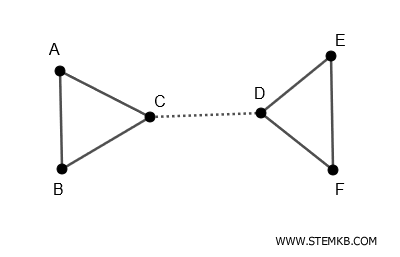
Tuttavia, anche se rimuoviamo il solo spigolo \( (C-D) \) il grafo si disconnette in due parti.

Quindi, anche l'insieme $ \{  (C-D) \} $ è un insieme di disconnessione del grafo.

Non essendoci un insieme di disconnessione più piccolo di {(A-C)} possiamo concludere che quest'ultimo è anche un cutset del grafo.

Viceversa, l'nsieme {(A-B), (B-C)} è un insieme di disconnessione ma non è un cutset.

In generale, quando un cutset è composto da un solo spigolo si parla di ponte.

In sintesi, un cutset è un insieme di spigoli la cui rimozione minima è sufficiente a disconnettere un grafo connesso.

E' uno strumento essenziale per l'analisi della connettività e della robustezza delle reti.