Il grafo orientabile

Un grafo orientabile è un grafo in cui puoi assegnare una direzione a ciascun arco in modo che il digrafo (cioè il grafo orientato risultante) sia fortemente connesso.

Dire che un grafo è fortemente connesso significa che da qualsiasi vertice è possibile raggiungere ogni altro vertice seguendo la direzione degli archi.

La connessione forte implica che, una volta orientato, esiste un percorso diretto da ogni vertice a qualsiasi altro vertice.

Un esempio

Immagina di avere un grafo connesso formato da 5 vertici, chiamati A, B, C, D, e E, e da archi che collegano alcune coppie di questi vertici.

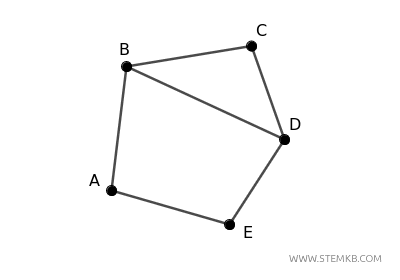
Questo grafo è orientabile perché puoi assegnare una direzione a ciascun arco e ottenere un grafo orientato fortemente connesso.

Ad esempio, supponi di orientare gli archi così:

• Da \( A \) a \( B \) (freccia \( A \rightarrow B \))
• Da \( B \) a \( C \) (freccia \( B \rightarrow C \))
• Da \( C \) a \( D \) (freccia \( C \rightarrow D \))
• Da \( D \) a \( E \) (freccia \( D \rightarrow E \))
• Da \( E \) a \( A \) (freccia \( E \rightarrow A \))
• Da \( B \) a \( D \) (freccia \( B \rightarrow D \))

Il risultato finale è un digrafo fortemente connesso, perché partendo da qualsiasi vertice, puoi raggiungere ogni altro vertice del digrafo seguono la direzione degli archi.

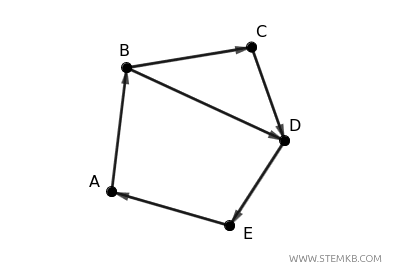
Per esempio, da \( A \) puoi raggiungere \( C \) passando per \( B \), o raggiungere \( E \) passando attraverso gli altri nodi.

Quindi, il grafo iniziale è un grafo orientabile.

Il teorema di Robbins

Secondo il Teorema di Robbins, un grafo connesso è orientabile se e solo se ogni arco appartiene ad almeno un ciclo.

Questa condizione è necessaria e sufficiente: ogni arco del grafo deve far parte di un ciclo per poter essere orientato in modo che il grafo risultante sia fortemente connesso.

Ciò significa che non deve esserci nessun arco "pendente" o isolato in termini di connettività ciclica: ogni arco deve poter essere percorso come parte di un percorso chiuso (ciclo).

Esempio

Il grafo con 5 vertici dell'esempio precedente è orientabile perché ogni arco appartiene ad almeno un ciclo.

 

Per esempio, il ciclo \( A \)-\( B \)-\( C \)-\( D \)-\( E \)-\( A \) include tutti gli archi principali che collegano i vertici in una struttura circolare.

 

In alternativa, puoi anche orientare gli archi in modo diverso e ottenere due cicli distinti A-B-D-E-A e B-D-C-B

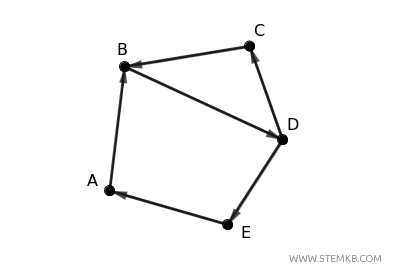
Anche in questo caso tutti gli archi del digrafo fanno parte di un ciclo.

Pertanto, ci sono ben due buone ragioni per affermare che il grafo è orientabile.

Dimostrazione del teorema

Vediamo come può essere dimostrato questo teorema.

1. Condizione necessaria: se un arco non appartenesse ad alcun ciclo, allora quell'arco costituirebbe una sorta di "collo di bottiglia" per il grafo. Questo arco isolato separerebbe potenzialmente i vertici in modo che una volta orientato, il grafo non potrebbe mai essere fortemente connesso.

2. Condizione sufficiente: partendo da un ciclo qualsiasi nel grafo, puoi orientare i suoi archi in modo ciclico. Poi, per ogni nuovo arco che non appartiene ancora a un ciclo orientato, puoi considerare un altro ciclo che include quest'arco e lo orienti ciclicamente, rispettando le direzioni già stabilite degli altri archi condivisi con altri cicli. Continuando con questo processo, alla fine tutti gli archi sareanno orientati, mantenendo la connessione del grafo.

La presenza di cicli, quindi, non solo facilita la navigabilità del grafo ma anche la sua trasformazione in una struttura direzionata solida e completamente connessa.

Questo tipo di orientabilità è cruciale in applicazioni come il design di reti di comunicazione e sistemi di trasporto, dove è necessario che ogni nodo (o punto) sia accessibile da ogni altro nodo senza eccezioni.