Grafo completo

Un grafo $ G = (V, E) $ è detto grafo completo se, per ogni coppia di vertici $ u, v \in V $, esiste un arco $ (u, v) \in E $.

In altre parole un grafo completo è un tipo di grafo in cui ogni coppia di vertici è collegata da un arco.

Se il grafo è diretto, ogni coppia di vertici $ (u, v) $ è connessa da un arco in entrambe le direzioni.

Immagina di essere a una festa dove conosci ogni singola persona: questo è l'equivalente di un grafo completo. Tutti parlano con tutti, nessuno escluso!

A cosa servono i grafi completi?

I grafi completi sono utilizzati in problemi di ottimizzazione, come il problema del commesso viaggiatore, dove si cerca il percorso più breve che visita ogni città (vertice) esattamente una volta.

Quanti archi ci sono in un grafo completo?

Formalmente, in un grafo completo con $ n $ vertici, ci sono esattamente $ \frac{n(n-1)}{2} $ archi, perché ogni vertice è connesso a tutti gli altri.

Questa formula deriva dal fatto che ogni vertice può essere connesso a n−1n−1 altri vertici, ma ogni arco viene contato due volte (una volta per ciascuno dei due vertici che collega), quindi dobbiamo dividere per 2.

Esempio pratico

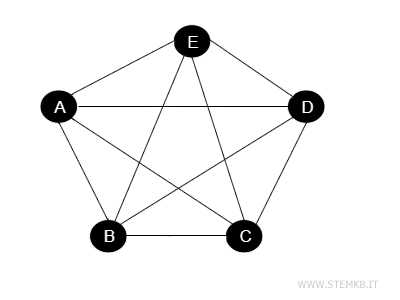
Prendiamo un grafo con 5 vertici: A, B, C, D, E.

In un grafo completo:

A sarà collegato a B, C, D e E
B sarà collegato a A, C, D e E
C sarà collegato a A, B, D e E
D sarà collegato a A, B, C e E.

In totale, ci saranno 10 archi ($ \frac{5(5-1)}{2} = 10 $).

Ecco la rappresentazione grafica.

esempio di grafo completo con 5 vertici

Il numero degli archi cresce in modo più che proporzionale al crescere dei vertici.

La formula $ \frac{n(n-1)}{2} $ mostra che il numero di archi cresce quadraticamente rispetto al numero di vertici. Ad esempio:

Per $ n = 2 $, abbiamo $ E = \frac{2(2-1)}{2} = 1 $ arco.
Per $ n = 3 $, abbiamo $ E = \frac{3(3-1)}{2} = 3 $ archi.
Per $ n = 4 $, abbiamo $ E = \frac{4(4-1)}{2} = 6 $ archi.
Per $ n = 5 $, abbiamo $ E = \frac{5(5-1)}{2} = 10 $ archi.
Per $ n = 6 $, abbiamo $ E = \frac{6(6-1)}{2} = 15 $ archi.
Per $ n = 7 $, abbiamo $ E = \frac{7(7-1)}{2} = 21 $ archi.
Per $ n = 8 $, abbiamo $ E = \frac{8(8-1)}{2} = 28 $ archi.
Per $ n = 9 $, abbiamo $ E = \frac{9(9-1)}{2} = 36 $ archi.
Per $ n = 10 $, abbiamo $ E = \frac{10(10-1)}{2} = 45 $ archi.

Come si può notare a colpo d'occhio, il numero di archi cresce rapidamente al crescere del numero di vertici.

Ecco il diagramma cartesiano che mostra il numero di archi in funzione del numero di vertici $(n)$ per che va da 3 a 10 in un grafo completo.

il numero degli archi in grafo completo al variare del numero dei nodi

Se provi a disegnare un grafo completo con un numero elevato di vertici, preparati a un disastro di linee intrecciate! Se non ci credi, prova a disegnare un grafo completo con 10 vertici e vedrai che confusione.

In sintesi, un grafo completo rappresenta una rete dove non c'è angolo oscuro: tutto è interconnesso. È l'esempio perfetto di connettività totale, sia in teoria che in pratica.