Cammino in un grafo

Un cammino in un grafo è una sequenza finita di archi i cui vertici sono distinti, tale che ogni coppia di archi consecutivi nella sequenza condivide un vertice comune.

In altre parole, un cammino non passa più di una volta per lo stesso vertice, escludendo eventualmente il vertice iniziale e finale nel caso di cammini chiusi (o cicli).

Ogni vertice nel grafo appare al massimo una volta lungo il cammino.

Un cammino con vertici \( v_1, v_2, \ldots, v_n \) può essere rappresentato come una sequenza di vertici \( (v_1, v_2, \ldots, v_n) \) o come una sequenza di archi \( (e_1, e_2, \ldots, e_{n-1}) \), dove ogni arco \( e_i \) ha vertici estremi \( v_i \) e \( v_{i+1} \).

Esempio

Immaginiamo un grafo composto da 5 vertici (A,B,C,D,E) e 7 spigoli (AB,AC,BC,BD,CE,CD,DE).

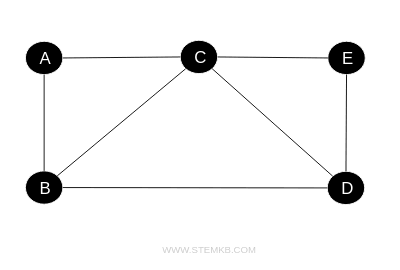
Ora, se vogliamo definire un cammino che inizia dal vertice A e termina al vertice D, potremmo scegliere la seguente sequenza di vertici: $ A \rightarrow B \rightarrow C \rightarrow D $

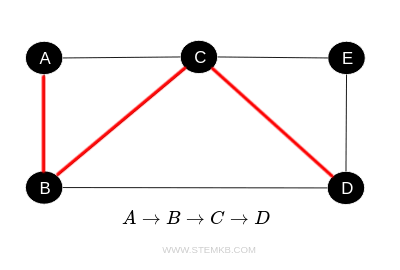
Questo cammino è rappresentato dalla sequenza di vertici A, B, C, D e dalla sequenza di archi AB, BC, CD.

Ogni vertice è visitato una sola volta, il che lo rende un cammino semplice. In questo caso, il cammino non è chiuso perché inizia e termina in vertici differenti.

Un altro cammino che connette i nodi A e D è il seguente: $ A \rightarrow C \rightarrow E \rightarrow D $

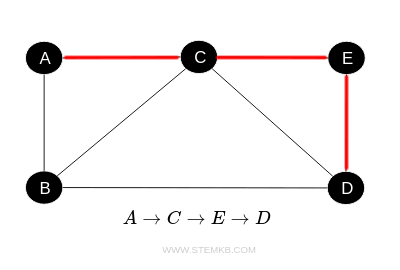
Se volessimo invece creare un cammino chiuso che inizia e finisce allo stesso vertice, potremmo avere: $ A \rightarrow B \rightarrow D \rightarrow C \rightarrow A $

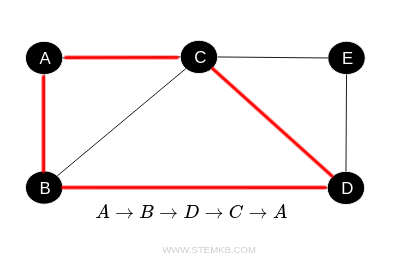
Questo è ancora un cammino perché ogni vertice è visitato una sola volta, tranne per il vertice A che è sia il punto di partenza che il punto di arrivo.