La differenza tra passeggiata, sentiero e cammino in un grafo
Una passeggiata o percorso (walk) è una sequenza finita di archi in cui ogni gli archi consecutivi sono adiacenti o identici (cappi) $$ v_0 \rightarrow v_1 \rightarrow v_2 \rightarrow ... \rightarrow v_n $$ Si può anche indicare in questo modo più compatto $$ v_0, v_1, v_2, ... , v_n $$ La lunghezza o cardinalità di una passeggiata è determinato dal numero di archi/spigoli di cui è composto.
In un percoso i vertici e gli archi possono essere ripetuti.
Se il primo e l'ultimo vertice della passeggiata coincidono $ v_0 = v_n $ si parla di passeggiata chiusa o circuito.
Ad esempio, questo grafo è composto da 4 vertici e 5 lati (spigoli). La sequenza A,B,C,A,B,D è un esempio di passeggiata. La lunghezza della passeggiata è 5 perché ci sono cinque archi nel percorso. Nota che i vertici A, B sono ripetuti e anche il lato AB è ripetuto nella sequenza.
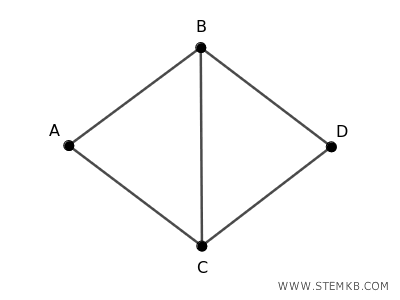
Il percorso A,B,C,A,B,D,C,A è invece una passeggiata chiusa perché il primo e l'ultimo vertice coincidono (A).
Una passeggiata in cui tutti gli archi sono distinti è detta "sentiero" o traccia" (trail).
In un sentiero il primo e l'ultimo arco possono anche essere uguali $ v_0 = v_n $, in questo caso si parla di sentiero chiuso.
Ad esempio, la sequenza B,C,A,B,D è un esempio di sentiero. In questo caso nella sequenza non viene ripetuto nessun arco. Nota che in un sentiero i vertici possono anche essere ripetuti. Nella sequenza che hai appena visto il vertice B si ripete due volte.

Il percorso A,B,C,A,B,D,C,A è invece una passeggiata chiusa perché il primo e l'ultimo vertice coincidono (A).
Una passeggiata in cui tutti i vertici sono distinti è detta cammino (path).
Anche in questo caso il primo e l'ultimo vertice di un cammno possono essere uguali $ v_0 = v_n $ si parla di cammino chiuso o ciclo.
Ad esempio, la sequenza A,B,D,C è un cammino perché i vertici non si ripetono nella sequenza.

Il percorso A,B,D,C,A è invece un ciclo o cammino chiuso perché il primo e l'ultimo vertice coincidono (A).
Quindi, i sentieri e i cammino sono dei sottoinsiemi dei percorsi.

