Le frazioni

Le frazioni sono un modo semplice per rappresentare parti di un tutto.

Immagina di tagliare una torta in 4 parti uguali: non sempre puoi esprimere la quantità di torta con numeri interi, ed è qui che le frazioni ti aiutano. Ogni singola fetta rappresenta $ \frac{1}{4} $ (un quarto) del totale.

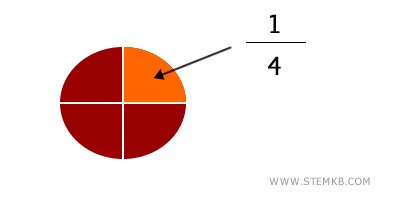
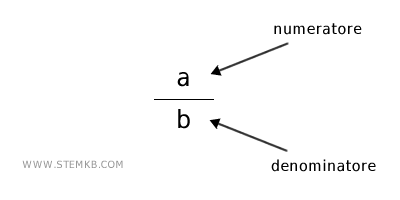
Una frazione è composta da due numeri fondamentali, ognuno con un ruolo ben preciso: 

• Numeratore: È il numero in alto nella frazione e indica quante parti dell'intero stiamo considerando. Ad esempio, in \( \frac{1}{4} \), il numeratore "1" significa che stai prendendo tre parti di qualcosa diviso in quattro.
• Denominatore: Si trova nella parte inferiore e indica il numero totale delle parti uguali in cui è stato diviso l'intero. Nel caso di \( \frac{1}{4} \), il denominatore "4" ti dice che l'intero è stato suddiviso in quattro parti uguali.

Questa struttura ti permette di rappresentare facilmente porzioni di un intero e rende più chiaro il rapporto tra le parti e il tutto.

A cosa servono le frazioni? Le frazioni sono utili nella vita di tutti i giorni per suddividere oggetti o quantità in parti uguali. Che si tratti di una torta, di un gruppo di persone o di una quantità di tempo, le frazioni ci aiutano a descrivere esattamente quanto ne consideriamo rispetto al totale. Quindi, comprendere le frazioni è fondamentale per affrontare concetti più avanzati in matematica, come le percentuali, i decimali e l'algebra.

Tipologie di frazioni

Esistono diversi tipi di frazioni

• Frazioni proprie: Il numeratore è più piccolo del denominatore, quindi rappresentano una parte minore di uno. Ad esempio, \( \frac{2}{3} \) indica che hai preso 2 delle 3 parti uguali in cui è stata divisa una torta.
• Frazioni improprie: In questo caso, il numeratore è maggiore del denominatore, quindi la frazione rappresenta una quantità superiore a uno. Queste frazioni possono essere convertite in un numero intero più una frazione. Ad esempio, \( \frac{23}{5} \) diventa \( 4 \frac{3}{5} \), ovvero 4 interi e 3 parti su 5.
• Frazioni apparenti: Quando il numeratore è uguale o multiplo del denominatore, la frazione rappresenta un numero intero. Un esempio è \( \frac{12}{3} \), che equivale a 4. In questo caso, non ha senso tagliare ulteriormente l’intero, poiché la divisione sarebbe perfettamente uniforme.

Ricorda che una frazione con lo zero al denominatore non ha significato, perché la divisione per zero non viene considerata un'operazione valida in matematica $$ \frac{a}{0} \quad \text{non valida} \ \ con \ a>0 $$ Ad esempio, non puoi scrivere $$ \frac{0}{0}  \ , \ \frac{1}{0} \ , \ \frac{2}{0} \ , ... $$ Viceversa, puoi scrivere \(\frac{0}{n}\) perché \(0\) diviso per un numero diverso da zero è sempre \(0\). $$ \frac{0}{1} = \frac{0}{2} = ...  \frac{0}{n} = 0 $$

Operazioni con le frazioni

Espoloriamo le regole essenziali delle frazioni facendo esempi concreti.

• Somma e sottrazione di frazioni
  Quando devi sommare o sottrarre frazioni, il primo passo è uniformare i denominatori, cioè il numero che si trova sotto la linea di frazione. Se i denominatori sono diversi, non puoi semplicemente sommare i numeratori; devi prima trovare un denominatore comune. Prendi come esempio \( \frac{1}{4} \) e \( \frac{2}{3} \). Per sommarle, porta entrambe a denominatore 12, il minimo comune multiplo di 4 e 3: $$ \frac{1}{4} + \frac{2}{3} = \frac{3}{12} + \frac{8}{12} = \frac{11}{12} $$ Questa semplice tecnica è alla base di molte operazioni matematiche.
• Moltiplicazione di frazioni
  La moltiplicazione tra frazioni è decisamente più semplice rispetto alla somma e alla sottrazione, poiché non richiede di uniformare i denominatori. Si moltiplicano direttamente numeratore per numeratore e denominatore per denominatore. Ad esempio: $$  \frac{2}{3} \times \frac{3}{5} = \frac{2 \times 3}{3 \times 5} = \frac{6}{15} = \frac{2}{5} $$ Questa operazione è utile in molti ambiti.
• Divisione di frazioni
  La divisione tra frazioni richiede un piccolo passaggio in più rispetto alla moltiplicazione: si deve infatti moltiplicare la prima frazione per il reciproco della seconda. Il reciproco si ottiene invertendo numeratore e denominatore. Vediamo un esempio pratico: $$ \frac{3}{4} \div \frac{2}{5} = \frac{3}{4} \times \frac{5}{2} = \frac{15}{8} $$

Frazioni e numeri decimali

Le frazioni e i numeri decimali sono due facce della stessa medaglia. Ogni frazione può essere convertita in un numero decimale dividendo il numeratore per il denominatore.

Alcune frazioni, come \( \frac{1}{2} \), si traducono in decimali esatti (\( 0.5 \)), mentre altre, come \( \frac{1}{3} \), generano decimali periodici (\( 0.333\ldots \)).

Vediamo qualche esempio pratico.

Ad esempio, la frazione \( \frac{25}{4} \) è una divisione che termina con un resto nullo ( \( r=0 \) ) e un numero decimale finito come quoziente ( \( 6.25 \) ).

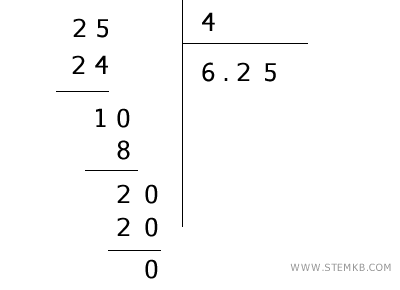
Ad esempio, la frazione \( \frac{455}{63} \) è una divisione che non si conclude mai con un resto uguale a zero. Questo significa che il quoziente ( \(7.\overline{2}=7.222222... \) è un numero decimale periodico, con un blocco di cifre (3) che si ripete illimitatamente nella parte decimale.

Questa connessione tra frazioni e decimali è particolarmente utile in ambiti come la finanza, dove i tassi di interesse e gli sconti sono spesso espressi in percentuali decimali.

Come capire se una frazione genera un numero decimale finito o periodico?

Puoi capirlo scomponendo in fattori primi il denominatore $ b $ della frazione \( \frac{a}{b} \) ridotta ai minimi termini.

• Se $ b = 1 $ la frazione genera un numero intero ( es. \( \frac{5}{1} = 5 \) ).
• Se $ b $ è composto da potenze di $ 2 $ e/o $ 5 $ è un numero decimale finito ( es. \( \frac{2}{5} = 2.5 \) ).
• Se $ b $ è composto da potenze diverse da $ 2 $ e $ 5 $ è un numero decimale periodico ( es. \( \frac{1}{3} = 0.333333... \) )..
• Se $ b $ è composto sia da potenze di $ 2 $ e/o $ 5 $ che di altri numeri primi, è un numero decimale periodico con un antiperiodo ( es. \( \frac{1}{6} = \frac{1}{2 \cdot 3} 0.1666666... \) ).

Confronto tra frazioni: chi è il più grande?

Confrontare frazioni è un’operazione che torna utile in molte situazioni quotidiane, come la ripartizione di cibo o denaro.

Per confrontare frazioni con denominatori diversi, bisogna prima portarle allo stesso denominatore, poi confrontare i numeratori.

Per esempio, prendi \( \frac{3}{8} \) e \( \frac{5}{12} \). Il minimo comune denominatore è 24, quindi:

$$ \frac{3}{8} = \frac{9}{24}, \quad \frac{5}{12} = \frac{10}{24} $$

In questo caso, \( \frac{10}{24} \) è maggiore di \( \frac{9}{24} \), quindi puoi concludere che \( \frac{5}{12} \) è più grande di \( \frac{3}{8} \).

In alternativa, puoi confrontare due frazioni utilizzando il principio delle proporzioni senza trovare un denominatore comune.

La regola afferma che il prodotto degli estremi è uguale al prodotto dei medi in una proporzione.

Se hai due frazioni \(\frac{a}{b}\) e \(\frac{c}{d}\), puoi confrontarle calcolando il prodotto degli estremi $ a \cdot d $ e il prodotto dei medi $ b \cdot c $

• Se \(a \cdot d > c \cdot b\), allora \(\frac{a}{b} > \frac{c}{d}\).
• Se \(a \cdot d < c \cdot b\), allora \(\frac{a}{b} < \frac{c}{d}\).

Ad esempio, confronta \(\frac{3}{8}\) e \(\frac{5}{12}\) utilizzando questa regola. Scrivi la proporzione:

$$ 3:8 = 5:12 $$

Ora calcola il prodotto degli estremi

$$ 3 \cdot 12 = 36 $$

Poi calcola il prodotto dei medi:

$$ 5 \cdot 8 = 40 $$

Poiché $ 36 < 40 $ puoi dedurre che:

$$ \frac{3}{8} < \frac{5}{12} $$

Questo metodo è molto più veloce ed evita il calcolo del minimo comune denominatore.