La divisione

La divisione è un'operazione matematica che ti dice quante volte un numero (dividendo) contiene un altro numero (divisore). Il risultato si chiama quoziente.

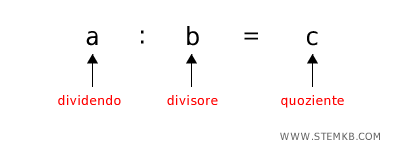
Quindi, il quoziente (c) è quel numero che moltiplicato al divisore (b) dà come risultato il dividendo (a): $$ c \times b = a $$

Ad esempio, se hai 12 caramelle e 3 amici, e vuoi distribuire equamente le caramelle, fai:

$$ 12 \div 3 = 4 $$

Ogni amico riceve 4 caramelle. Il 12 è il dividendo, il 3 è il divisore, e il risultato 4 è il quoziente.

In questo caso 12 è il dividendo, 3 è il divisore e 4 è il quoziente.

Tuttavia, non sempre la divisione intera è possibile, perché ci sono situazioni in cui il dividendo non è un multiplo esatto del divisore. In questi casi, otteniamo un resto oppure, se vogliamo una divisione esatta, entriamo nel mondo dei numeri frazionari o decimali.

La divisione con resto

Quando dividi un numero che non è perfettamente divisibile con un altro,  rimane qualcosa che chiamiamo resto.

Ad esempio, il numero 14 non è divisibile per 3.

$$ 14 \div 3 $$

Il numero 3 non entra esattamente in 14. Entra 4 volte (perché 3×4=12), ma rimangono fuori 2 unità.

Quindi diciamo che 14 diviso 3 dà come risultato 4, con un resto di 2:

$$ 14 \div 3 = 4 \text{ con un resto di } 2 $$

Significa che puoi fare 4 gruppi di 3, e ti avanzano 2 unità.

La divisione con i decimali

Se vuoi evitare di avere un resto e vuoi una divisione precisa, puoi usare i numeri decimali.

Ad esempio, dividi 17 per 5

$$ 17 \div 5 $$

Anziché scrivere il risultato della divisione con il resto

$$ 17 \div 5 = 3 \text{ con un resto di } 2  $$

Puoi scrivere il quoziente con i decimali.

$$ 17 \div 5 = 3,4  $$

In questo caso, il risultato è un numero con la virgola, ovvero 3,4.

Questo significa che il numero 17 è stato diviso in 5 parti uguali e ogni parte vale 3,4 unità.

In altre parole, è una divisione esatta in termini decimali.

Come calcolare la divisione

Fare una divisione può sembrare complicato all'inizio, ma se segui un metodo chiaro e semplice, diventa un processo abbastanza meccanico.

Ti descrivo il metodo per la divisione in colonna, che è utile per dividere numeri grandi.

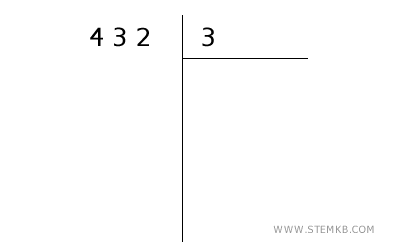
Immagina di dover dividere 432 per 3. Ecco i passaggi:

1. Scrivi il dividendo e il divisore
   In questo caso scrivi il dividendo (432) a sinistra e il divisore (3) a destra sopra la linea.
   
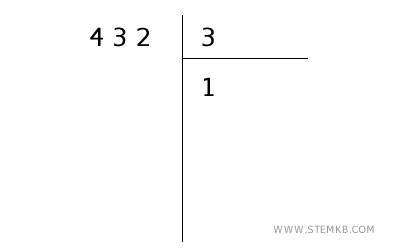
2. Dividi la prima cifra
   Guarda il primo numero a sinistra del dividendo: in questo caso, è 4. Chiediti: "quante volte 3 sta nel 4?" La risposta è 1.
   Quindi, scrivi 1 sotto la linea di divisione.
   
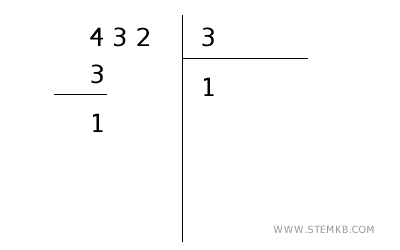
3. Moltiplica e sottrai
   Moltiplica 1 per 3, ottenendo 3, scrivi questo 3 sotto il 4 e sottrai: \( 4 - 3 = 1 \).
   
4. Porta giù la cifra successiva del dividendo
   Porta giù la cifra successiva del dividendo (3) e scrivila accanto al risultato della sottrazione, formando 13.
   
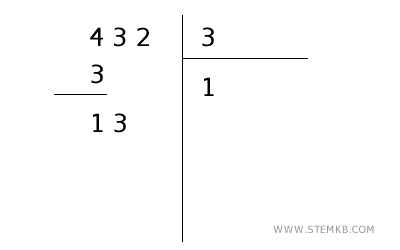
5. Dividi il nuovo numero
   Ora chiediti: "quante volte 3 sta nel 13?" La risposta è 4. Scrivi 4 sotto la linea del divisore, accanto al primo numero che hai già ottenuto.
   
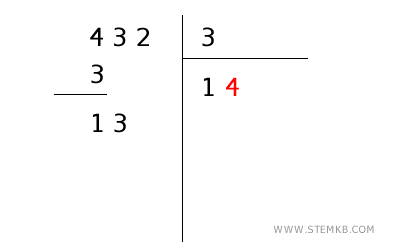
6. Moltiplica e sottrai di nuovo
   Moltiplica 4 per 3, ottenendo 12, scrivi 12 sotto il 13 e sottrai: \( 13 - 12 = 1 \).
   
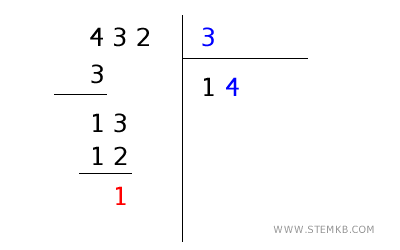
7. Porta giù la cifra successiva del dividendo
   Porta giù la cifra successiva del dividendo (2), formando 12.
   
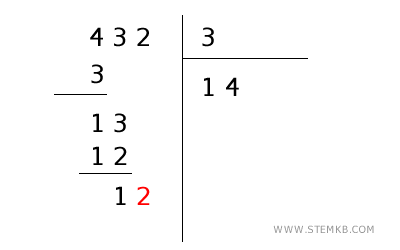
8. Dividi il nuovo numero
   Quante volte 3 sta in 12? Esattamente 4. Quindi, scrivi 4 sotto la linea del divisore, accanto ai numeri precedenti.
   
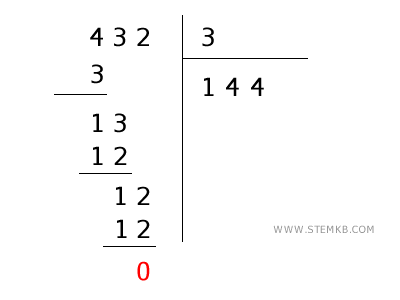
9. Moltiplica e sottrai di nuovo
   Moltiplica 4 per 3, che fa 12. Poi sottrai: \( 12 - 12 = 0 \). Poiché il resto è zero, la divisione termina qui. Il risultato della divisione è  \( 432 \div 3 = 144 \).
   

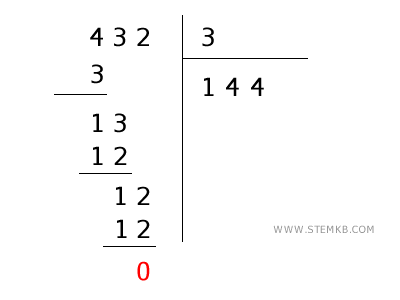
Questo metodo funziona per qualsiasi numero e ti permette di affrontare anche divisioni più complesse in modo sistematico.

Se l'ultima differenza è minore del divisore, aggiungi uno zero a destra della differenza e inserisci una virgola nel quoziente. Continua quindi il calcolo per ottenere la parte decimale del risultato desiderato o finché il resto è zero.

Esempio

Facciamo un esempio di divisione decimale con resto

Immagina di dividere 25 per 4:

1. Scrivi la divisione in colonna
   In questo caso il dividendo è 25 e il divisore è 4.
   
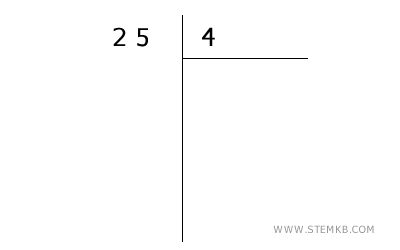
2. Svolgi la divisione in colonna
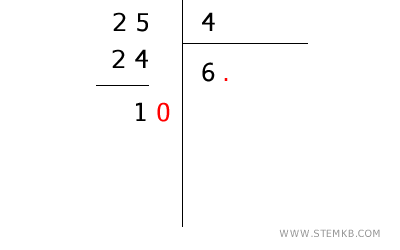
   Il 4 entra in 25 sei volte, perché \( 4 \times 6 = 24 \). Scrivi 6 sotto la linea del divisore e sottrai \( 25 - 24 = 1 \).
   
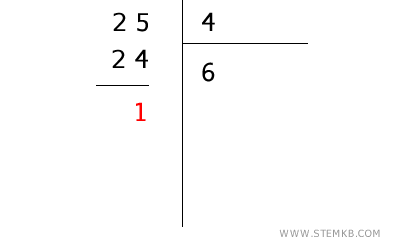
3. Il resto è minore del divisore
   A questo punto, 1 è più piccolo di 4. Per proseguire, aggiungi uno zero a destra della differenza, ottenendo 10. Poi, metti una virgola nel quoziente (dopo il 6) per indicare che stiamo entrando nella parte decimale.
   
4. Continua con la parte decimale
   Il 4 entra nel 10 due volte, perché \( 4 \times 2 = 8 \). Aggiungi 2 dopo la virgola nel quoziente, che diventa ora 6,2. Poi sottrai \( 10 - 8 = 2 \).
   
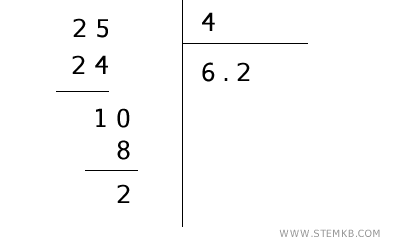
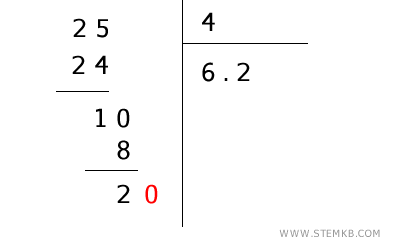
5. Ripeti il processo
   Ancora, il 2 è minore di 4, quindi aggiungi un altro zero, ottenendo 20.
   
   Il numero 4 sta in 20 cinque volte, quindi aggiungi 5 al quoziente, ottenendo 6,25. Sottrai \( 20 - 20 = 0 \), e non resta più nulla da dividere.
   

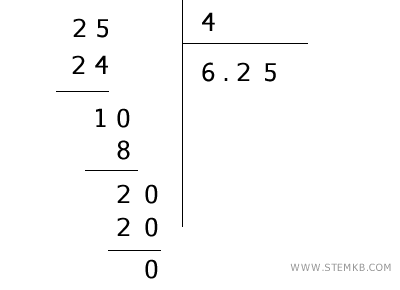
Il risultato della divisione è

$$ 25 \div 4 = 6,25 $$

In sintesi:

• Se la differenza è minore del divisore, aggiungi uno zero e continua a dividere.
• Continua fino a ottenere il risultato decimale desiderato o finché il resto diventa zero.

Questo metodo ti permette di ottenere la precisione decimale necessaria senza difficoltà.

Esempio (divisione a più cifre)

Quando il dividendo e il divisore sono numeri a più cifre, puoi semplificare il calcolo osservando le cifre più significative dei due numeri.

Ti faccio un esempio, dividi 455 per 63.

A questo punto potresti contare quante volte sta il 63 nel 455 ma potrebbe essere difficoltoso farlo a mente.

In alternativa, per semplificare il calcolo, osserva quante volte sta il 6 nel 45.

Dove 6 è la cifra più significativa del divisore (63) e 45 è la cifra più significativa del dividendo (455) in grado di contenere 6.

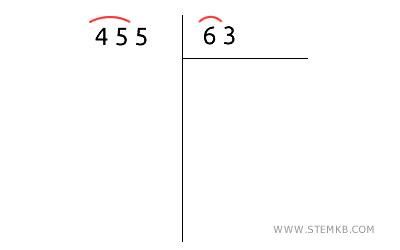
In questo caso il 6 sta 7 volte nel 45, quindi scrivi 7 nel quoziente.

Ora moltiplica il divisore 63 per 7 e scrivi il risultato 63x7=441 sotto il dividendo (455). 

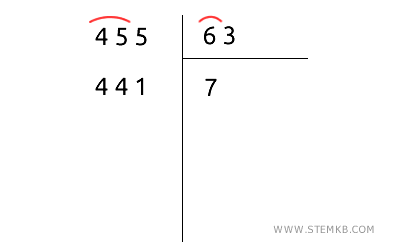
Poi calcola il resto 455-441=14.

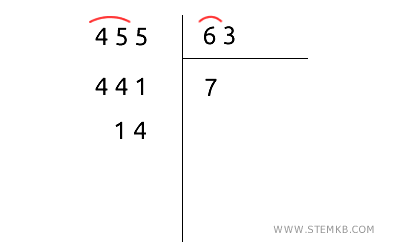
Hai così ottenuto il risultato della divisione, il divisore 63 sta 7 volte (quoziente) nel dividendo 455 con il resto di 14.

E ovviamente, se vuoi, puoi continuare a calcolare il quoziente come abbiamo visto nell'esempio precedente.

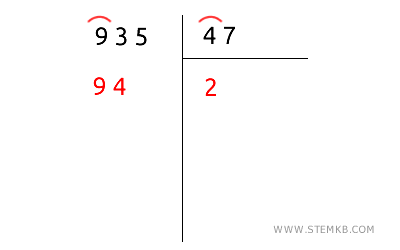
Ricorda che questo metodo semplifica il procedimento ma si basa su un calcolo approssimativo e non funziona sempre. Una volta effettuata la stima, è necessario considerare tutte le cifre del divisore per calcolare e confermare il risultato corretto, poiché la stima basata solo sulle prime cifre può essere fuorviante. Ad esempio, nella divisione 935 diviso 47, potresti iniziare verificando quante volte il 4 (la cifra più significativa di 47) entra nel 9 (la cifra più significativa di 935). Il 4 entra 2 volte nel 9. Tuttavia, se moltiplichi 2 per il divisore ottieni \( 2 \times 47 = 94 \), un risultato maggiore di 93. In questo caso, 2 non è un quoziente valido, poiché le cifre successive del divisore influenzano il calcolo.

Divisione con le frazioni

Una divisione puoi trasformarla in una frazione, ponendo il dividendo al numeratore e il divisore al denominatore.

Ad esempio, se hai 14 caramelle e 3 amici e vuoi dare a ciascuno una parte esatta, puoi scrivere la divisione $ 14 \div 3 = 4,67 $ oppure una frazione:

$$ \frac{14}{3} = 4,67 $$

Quindi, ogni amico riceve 4,67 caramelle.

Divisione come ripetuta sottrazione

Un altro modo di vedere la divisione: 12 diviso 3 significa togliere 3 da 12 fino a zero:

$$ 12 - 3 - 3 - 3 - 3 = 0 $$

Quindi 12 diviso 3 è 4, perché hai tolto 3 per 4 volte.

Il quoziente di due numeri relativi

Il quoziente tra due numeri interi ha valore assoluto pari al quoziente dei valori assoluti e segno positivo se i numeri sono concordi, negativo se discordi. È zero se il numeratore è zero e il denominatore è diverso da zero.

In termini pratici, se prendi \( a \) e \( b \) come numeri interi, con \( b \neq 0 \), il valore assoluto del quoziente \( \frac{a}{b} \) sarà uguale a \( \frac{|a|}{|b|} \).

Per il segno del quoziente devi utilizzare la stessa regola del segno della moltiplicazione.

• Il quoziente ha segno positivo (+) se i due numeri sono concordi (entrambi positivi o entrambi negativi)
• Il quoziente ha segno negativo (-) se i numeri sono discordi (uno positivo e l'altro negativo)

Ricorda che due numeri sono detti "concordi" se hanno lo stesso segno. Al contrario sono detti "discordi" se hanno un segno diverso. Ad esempio, 2 e 3 sono concordi. Anche -2 e -3 sono concordi, mentre 2 e -3 sono discordi.

Esempio

Ad esempio, svolgi la divisione seguente:

$$ 8 \div 2 $$

In questo caso il dividendo \( a = 8 \) e il divisore \( b = 2 \) sono entrambi positivi, quindi il segno del quoziente è positivo

$$ 8 \div 2 = 4 $$

In ogni caso il quoziente lo calcoli dividendo il valore assoluto del dividendo con il valore assoluto del divisore. Il segno, invece, dipende se i due numeri hanno lo stesso segno oppure no. $$ 8 \div 2 = + (|8| \div |2|)=+4 $$

Allo stesso modo anche se il dividendo e il divisore sono entrambi negativi, il risultato sarà positivo.

$$ (-8) \div (-2) = 4 $$

I due numeri sono concordi perché hanno entrambi il segno meno. Quindi, il segno del quoziente è positivo. $$ (-8) \div (-2) = +(|-8| \div |-2|) = +(8 \div 2) = +4 $$

Se, invece, i segni sono diversi, il segno del quoziente è negativo, perché i numeri sono discordi.

$$ (-8) \div  2 = -4 $$

$$ 8 \div (-2) = -4 $$

In entrambi i casi i due numeri sono discordi perché hanno un segno diverso. Quindi, il segno del quoziente è negativo. $$ (-8) \div 2 = -(|-8| \div |2|) = -(8 \div 2) = -4 $$ $$ 8 \div (-2) = -(|8| \div |-2|) = -(8 \div 2) = -4 $$

Infine, quando il numeratore è zero (cioè \( a = 0 \)) e il denominatore \( b \) è diverso da zero, il risultato è sempre zero.

$$ 0 \div 2 = 0 $$

$$ 0 \div (-2) = 0 $$

Seguendo queste semplici regole puoi calcolare il quoziente anche tra numeri interi di segno diverso.

Il quoziente dei numeri razionali

Il quoziente di due numeri razionali, dove il secondo è diverso da zero, equivale al prodotto del primo per il reciproco del secondo. $$ \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c} $$

I numeri razionali sono quei numeri che possono essere espressi come una frazione \( \frac{a}{b} \), dove \( a \) e \( b \) sono numeri interi e \( b \neq 0 \).

Per esempio, \( \frac{3}{4} \), \( -\frac{2}{5} \) e \( 7 \) che puoi scrivere come \( \frac{7}{1} \) sono tutti numeri razionali.

Quando vuoi calcolare il quoziente tra due numeri razionali, \( \frac{a}{b} \) e \( \frac{c}{d} \) (dove \( c \neq 0 \) per evitare una divisione per zero), puoi immaginare di scrivere questa operazione come:

$$ \frac{\frac{a}{b}}{\frac{c}{d}} $$

La divisione tra frazioni può sembrare complessa, ma in realtà si semplifica grazie a una proprietà fondamentale: dividere per una frazione equivale a moltiplicare per il suo reciproco.

$$ \frac{\frac{a}{b}}{\frac{c}{d}} = \frac{a}{b} \cdot \frac{d}{c}  = \frac{a \cdot d}{b \cdot c} $$

Dove il reciproco di una frazione è semplicemente una nuova frazione ottenuta invertendo numeratore e denominatore. Ad esempio, il reciproco di \( \frac{c}{d} \) è \( \frac{d}{c} \).

In altre parole, la divisione può essere pensata come un'operazione inversa alla moltiplicazione, e il concetto di reciproco ne è la chiave. Ci permette di lavorare con frazioni in modo più sistematico e di semplificare operazioni complesse.

Un esempio concreto

Immagina di voler calcolare questa divisione:

$$ \frac{3}{4} \div \frac{2}{5} $$

Riscrivi la divisione come un rapporto tra due frazioni.

$$ \frac{\frac{3}{4}}{\frac{2}{5}} $$

Ora applica la regola e moltiplica la prima frazione per il reciproco della seconda frazione.

$$ \frac{\frac{3}{4}}{\frac{2}{5}} = \frac{3}{4} \cdot \frac{5}{2} $$

Moltiplica numeratori e denominatori:

$$ \frac{3 \cdot 5}{4 \cdot 2} = \frac{15}{8} $$

Il risultato del quoziente è quindi \( \frac{15}{8} \)

Le proprietà della divisione

La divisione ha delle proprietà particolari che la differenziano da altre operazioni, come l'addizione o la moltiplicazione. Vediamole nel dettaglio:

• La proprietà invariantiva della divisione
  Se in una divisione moltiplichi o dividi sia il dividendo che il divisore per uno stesso numero \( k \neq 0 \), il quoziente rimane invariato. $$ \frac{a}{b} = \frac{a \cdot k}{b \cdot k} = \frac{a \div k}{b \div k} $$ Dove \( a \) è il dividendo, \( b \) è il divisore, e \( k \) è un numero diverso da zero.

  Esempio: Nella divisione $ 8 \div 4 $ se moltiplichi o dividi per due sia il dividendo che il divisore, il quoziente resta lo stesso.  $$  8 \div 4 = (8 \times 2) \div ( 4 \times 2) = (8 \div 2) \div ( 4 \div 2) = 2 $$ E' molto importante che il numero $ k $ sia sempre diverso da zero, per evitare di incappare in una divisione per zero.

• La proprietà distributiva della divisione si applica solo a destra
  La proprietà distribributiva della divisione rispetto all'addizione e alla moltiplicazione si applica solo a destra, ossia solo quando il divisore è applicato alla somma o alla sottrazione. Inoltre, il divisore deve essere sempre diverso da zero. $$ (a + b) : c = a : c + b : c $$ $$ (a - b) : c = a : c - b : c $$

  Esempio: Considera questa espressione $$ (8+4):2  $$ Puoi ottenere lo stesso risultato distribuendo il divisore a entrambi gli addendi  $$ (8+4):2 = (8:2) + (4:2)  $$ Se svolgi i calcoli ottieni lo stesso risultato in entrambi i lati dell'equazione $$ (8+4):2 = (8:2) + (4:2)  $$ $$ 12:2 = 4 + 2  $$ $$ 6 = 6 $$

• Non è commutativa
  La commutatività significa che cambiando l'ordine degli elementi l'operazione dà lo stesso risultato. Questo è vero per l'addizione e la moltiplicazione (ad esempio, \(2 + 3 = 3 + 2\)), ma non per la divisione.

  Esempio: $$  8 \div 4 = 2 $$ ma
  $$ 4 \div 8 = 0,5 $$ Quindi, l'ordine conta nella divisione, e cambiare l'ordine cambia il risultato.

• Non è associativa
  La proprietà associativa si applica quando possiamo cambiare il raggruppamento degli elementi senza alterare il risultato, come nell'addizione \((a + b) + c = a + (b + c)\). La divisione, invece, non è associativa.

  Esempio: $$ (24 \div 4) \div 2 = 6 \div 2 = 3 $$ ma $$ 24 \div (4 \div 2) = 24 \div 2 = 12 $$ In questo caso, cambiando il modo in cui associ i numeri, otteni risultati diversi. Quindi, è fondamentale rispettare l'ordine delle operazioni.

• Elemento neutro
  Nella divisione, il numero neutro è il numero 1*. Quando dividi un numero per 1, il risultato è sempre il numero stesso. Esempio: $$ 9 \div 1 = 9 $$ Questo è perché qualsiasi numero diviso per 1 rimane invariato.
• Divisione per zero impossibile
  Dividere un numero per zero non è possibile, né in matematica né nella realtà. La divisione per zero non ha significato, e per buoni motivi! Se potessimo dividere per zero, otterremmo risultati illogici e indefiniti.

  Esempio: Non possiamo calcolare: $$  8 \div 0 $$

• Divisione di zero
  Quando invece è zero ad essere diviso per un altro numero (diverso da zero), il risultato è sempre zero.

  Esempio: $$ 0 \div 5 = 0 $$ In sostanza, dividere zero per qualsiasi numero ti dà sempre zero.

• La divisione è un'operazione interna ai numeri razionali
  Questo significa che la divisione tra due numeri razionali restituisce sempre un altro numero razionale.

  Esempio: Dati due numeri razionali $ \frac{2}{3} $ e $ \frac{5}{7} $, la loro divisione è $$ \frac{2}{3} \div \frac{5}{7} = \frac{2}{3} \cdot \frac{7}{5} = \frac{2 \cdot 7}{3 \cdot 5} = \frac{14}{15} $$ Anche il quoziente $ \frac{14}{15} $ è un numero razionale.

• La divisione non è un'operazione interna ai numeri naturali e ai numeri interi
  La divisione non è un'operazione interna all'insieme dei numeri naturali \( \mathbb{N} \), in quanto il risultato della divisione di due numeri naturali non è sempre un numero naturale. Per la stessa ragione, non è un'operazione interna all'insieme dei numeri interi.
  

  Esempio: La divisione \( 5 \div 2 = 2.5 \) non appartiene all'insieme dei numeri naturali \( \mathbb{N} \), poiché i numeri naturali sono interi e non negativi. In questo esempio, il quoziente tra i due numeri naturali (5 e 2) è un numero razionale (2.5) $$ 5 \div 2 = 2.5 \in \mathbb{Q} $$ Quindi, il risultato non è un numero naturale $ 2.5 \notin \mathbb{N} $.