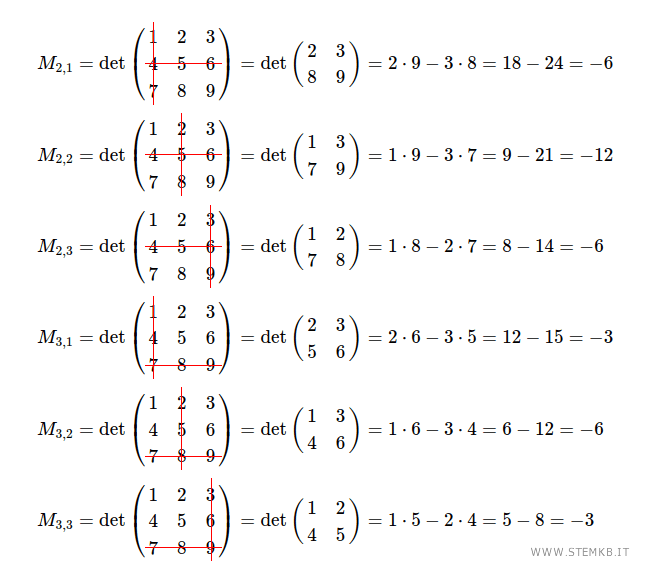Il minore di una matrice

In matematica, il "minore" di una matrice è il determinante di una sottomatrice quadrata che ottieni eliminando una o più righe e/o colonne.

Puoi calcolare i minori di una matrice sia sulle matrici quadrate che rettangolari.

Ogni matrice quadrata o rettangolare ha tanti minori, quante sono le sottomatrici quadrate che puoi estrarre.

A cosa servono i minori? I minori hanno diverse applicazioni in algebra lineare. Ad esempio, ti permettono di calcolare il determinante di una matrice di dimensioni 3x3 o 4x4 tramite il metodo di Laplace, oppure di trovare l'inversa di una matrice.

Per esempio, prendi una generica matrice 3x3 con tre righe e tre colonne

$$ M = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} $$

Elimina la seconda riga e la terza colonna e ottieni una sottomatrice quadrata S_2,3

$$ S_{2,3} \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \begin{pmatrix} a & b \\ g & h \end{pmatrix} $$

Il minore M_2,3 è il determinante della sottomatrice quadrata S_2,3

$$ M_{2,3} = \det \begin{pmatrix} a & b \\ g & h \end{pmatrix} = a \cdot h - b \cdot g $$

Utilizzando questo metodo puoi calcolare tutti i minori della matrice.

Ovviamente, puoi calcolare il determinante solo delle sottomatrici quadrate. Quindi, le sottomatrici rettangolari non considerarle.

Quanti sono i minori di una matrice 3x3?

Complessivamente una matrice 3x3 ha 19 minori

1 minore di ordine 3
E' il determinante della matrice stessa 3x3 $$ \det M = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} $$
9 minori di ordine 2
Sono i determinanti delle 4 matrici 2x2 che ottieni eliminando una riga e una colonna
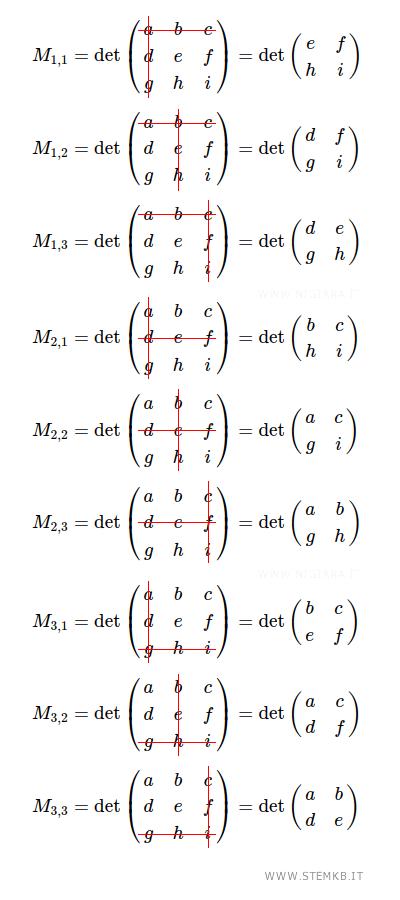
$i minordi di ordine 2 di una matrice 3x3 $$ M_{1,1} = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \det \begin{pmatrix} e & f \\ h & i \end{pmatrix} $$ $$ M_{1,2} = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \det \begin{pmatrix} d & f \\ g & i \end{pmatrix} $$ $$ M_{1,3} = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \det \begin{pmatrix} d & e \\ g & h \end{pmatrix} $$ $$ M_{2,1} = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \det \begin{pmatrix} b & c \\ h & i \end{pmatrix} $$ $$ M_{2,2} = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \det \begin{pmatrix} a & c \\ g & i \end{pmatrix} $$ $$ M_{2,3} = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \det \begin{pmatrix} a & b \\ g & h \end{pmatrix} $$ $$ M_{3,1} = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \det \begin{pmatrix} b & c \\ e & f \end{pmatrix} $$ $$ M_{3,2} = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \det \begin{pmatrix} a & c \\ d & f \end{pmatrix} $$ $$ M_{3,3} = \det \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} = \det \begin{pmatrix} a & b \\ d & e \end{pmatrix} $$$
9 minori di ordine 1
Sono i singoli elementi della matrice 3x3 che ottieni eliminando due righe e due colonne. Il determinante di un singolo elemento è uguale al valore dell'elemento stesso.

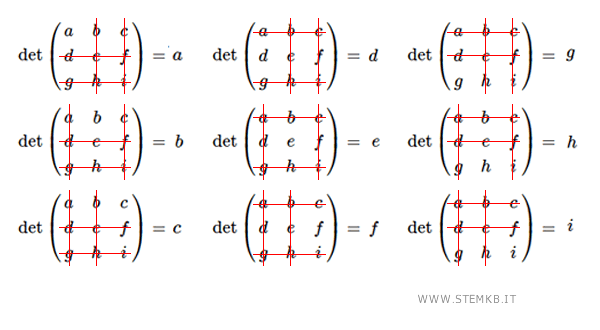
Se sommi tutti questi insieme, ottieni un totale di 9 + 9 + 1 = 19 minori.

Nota che il calcolo dei minori diventa sempre più complicato con l'aumentare delle dimensioni della matrice. Ad esempio, calcolare i minori di una matrice 4x4 richiede di calcolare il determinante di 16 diverse matrici 3x3 (minori di ordine 3), il determinante di 144 matrici di ordine 2x2 (minori di ordine 2) e il determinante dei 16 elementi della matrice (minori di ordine 1). Quindi, una matrice 4x4 ha ben 176 minori.

Ora facciamo un esempio pratico con una matrice numerica.

Considera questa matrice

$$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$

Il minore di ordine 3 della matrice M è il determinante della matrice stessa.

In questo caso il determinante della matrice quadrata 3x3 è uguale a zero.

$$ \det M = \det \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$$

$$ \det M = 1 \cdot 5 \cdot 9 + 2 \cdot 6 \cdot 7 + 3 \cdot 4 \cdot 8 - 3 \cdot 5 \cdot 7 - 2 \cdot 4 \cdot 9 - 1 \cdot 6 \cdot 8$$

$$ \det M = 0 $$

I minori di ordine 2 della matrice M li ottieni calcolando i determinanti delle sottomatrici quadrate 2x2

Il minore M_1,1 è il determinante della sottomatrice quadrata 2x2 che ottieni eliminando la prima riga e la prima colonna

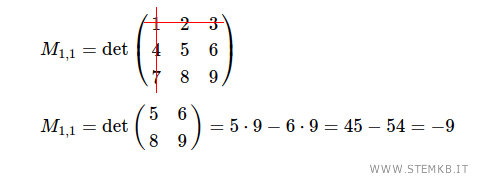
esempio di calcolo del minore

Il minore M_1,2 è il determinante della sottomatrice quadrata 2x2 che ottieni eliminando la prima riga e la seconda colonna

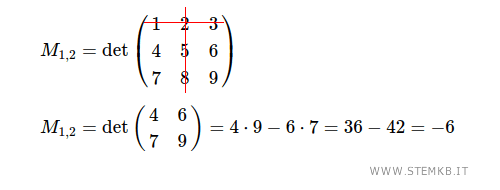
esempio di calcolo del minore M1,2

Il minore M_1,3 è il determinante della sottomatrice quadrata 2x2 che ottieni eliminando la prima riga e la terza colonna

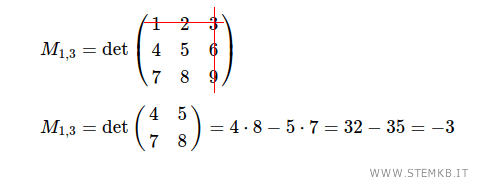
calcolo del minore M1,3

E via dicendo puoi calcolare gli altri minori di ordine 2 della matrice M.

gli altri minori di ordine 2 della matrice