Un grafo bipartito ha cicli di lunghezza pari
Un grafo \( G \) è bipartito se e solo se ogni ciclo di \( G \) ha lunghezza pari.
Un grafo è un insieme di vertici collegati da spigoli (o archi).
Un grafo è bipartito se possiamo dividere i suoi vertici in due insiemi disgiunti \( A \) e \( B \) in modo che ogni spigolo colleghi un vertice di \( A \) con un vertice di \( B \).
In altre parole, non ci sono spigoli che collegano due vertici all'interno dello stesso insieme \( A \) o \( B \).
Esempio
Facciamo un esempio pratico per chiarire il concetto.
Supponiamo di avere un grafo con i seguenti vertici e spigoli:
- Vertici: \( \{A, B, C, D, E, F\} \)
- Spigoli: \( \{(A, B), (A, D), (B, C), (C, D), (D, E), (E, F)\} \)
Proviamo a dividere i vertici in due insiemi \( X = \{A, C, E\} \) e \( Y = \{B, D, F\} \) in modo che ogni spigolo colleghi un vertice di \( X \) con un vertice di \( Y \).
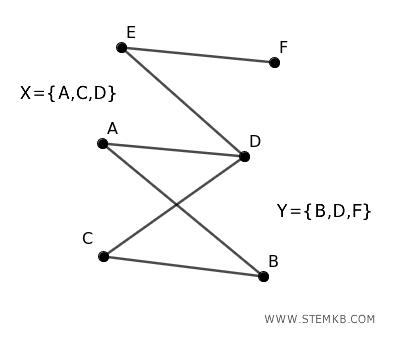
Verifichiamo gli spigoli uno a uno:
- (A, B) → \( A \) è in \( X \) e \( B \) è in \( Y \)
- (A, D) → \( A \) è in \( X \) e \( D \) è in \( Y \)
- (B, C) → \( B \) è in \( Y \) e \( C \) è in \( X \)
- (C, D) → \( C \) è in \( X \) e \( D \) è in \( Y \)
- (D, E) → \( D \) è in \( Y \) e \( E \) è in \( X \)
- (E, F) → \( E \) è in \( X \) e \( F \) è in \( Y \)
Ogni spigolo collega un vertice di \( X \) con un vertice di \( Y \), quindi il grafo è bipartito.
Ora prendiamo il ciclo $ A \to B \to C \to D \to A $ in questo grafo.

Analizziamo gli spigoli singolarmente:
- A → B: A è in \( X \), B è in \( Y \)
- B → C: B è in \( Y \), C è in \( X \)
- C → D: C è in \( X \), D è in \( Y \)
- D → A: D è in \( Y \), A è in \( X \)
Il ciclo ha lunghezza 4 ovvero ha una lunghezza pari.
Esempio di grafo non bipartito
Consideriamo ora un grafo con i seguenti vertici \( \{P, Q, R, S\} \) e spigoli: \( \{(P, Q), (Q, R), (R, S), (S, P), (P, R)\} \)
Proviamo a dividere i vertici in due insiemi \( X = \{P, R\} \) e \( Y = \{Q, S\} \):

Verifichiamo gli spigoli:
- (P, Q) → \( P \) è in \( X \) e \( Q \) è in \( Y \)
- (Q, R) → \( Q \) è in \( Y \) e \( R \) è in \( X \)
- (R, S) → \( R \) è in \( X \) e \( S \) è in \( Y \)
- (S, P) → \( S \) è in \( Y \) e \( P \) è in \( X \)
- (P, R) → \( P \) è in \( X \) e \( R \) è in \( X \) e si verifica un problema perché entrambi sono nello stesso insieme
In questo grafo abbiamo lo spigolo (P,R) che collega due vertici nello stesso insieme X, quindi il grafo non è bipartito.
Infatti, in questo grafo ci sono cicli di lunghezza dispari. Ad esempio $ P \to Q \to R \to P $ dove l'estremo iniziale e finale uguale si conta una sola volta.
La presenza di un ciclo dispari anche in presenza di altri cicli pari indica che il grafo non può essere bipartito. Ad esempio, se aggiungiamo al grafo il lato (Q,S) introduciamo un ciclo $ P \to Q \to S \to R \to P $ di lunghezza pari nel grafo. Tuttavia, la presenza dei cicli dispari PQR e PRS indica che il grafo non è bipartito.

In conclusione, un grafo è bipartito se possiamo dividere i suoi vertici in due insiemi tali che ogni spigolo collega un vertice di un insieme con un vertice dell'altro insieme.
In questo caso, ogni ciclo nel grafo avrà lunghezza pari. Se c'è anche un solo ciclo di lunghezza dispari, il grafo non può essere bipartito.
Dimostrazione
La dimostrazione è suddivisa in due parti:
Parte 1: Se \( G \) è bipartito, allora ogni ciclo ha lunghezza pari.
Se \( G \) è bipartito, possiamo dividere i vertici in due insiemi \( A \) e \( B \) tali che ogni spigolo collega un vertice di \( A \) con uno di \( B \).
Supponiamo di avere un ciclo \( v_0 \to v_1 \to \ldots \to v_n \to v_0 \).
Supponiamo che \( v_0 \) sia in \( A \). Allora:
- \( v_1 \) sarà in \( B \)
- \( v_2 \) sarà in \( A \)
- \( v_3 \) sarà in \( B \)
- e così via...
Poiché \( v_n \) deve essere in \( B \) e poi tornare a \( v_0 \) che è in \( A \), il numero di passaggi (o spigoli) nel ciclo deve essere pari.
Quindi, il ciclo ha lunghezza pari.
Parte 2: Se ogni ciclo ha lunghezza pari, allora \( G \) è bipartito
Supponiamo che ogni ciclo di \( G \) abbia lunghezza pari.
Scegliamo un vertice \( v \) e definiamo due insiemi:
- \( A \): insieme di vertici \( w \) per i quali il percorso più breve da \( v \) a \( w \) ha lunghezza pari.
- \( B \): insieme di vertici \( w \) per i quali il percorso più breve da \( v \) a \( w \) ha lunghezza dispari.
Se due vertici in \( A \) fossero adiacenti, ci sarebbe un ciclo di lunghezza dispari (percorso da \( v \) a ciascuno dei due vertici più l'arco tra loro).
Poiché ogni ciclo ha lunghezza pari, non ci possono essere due vertici in \( A \) adiacenti, e lo stesso vale per \( B \).
Quindi, ogni arco deve collegare un vertice di \( A \) con un vertice di \( B \), il che significa che \( G \) è bipartito.
Conclusione
Un grafo è bipartito se e solo se ogni ciclo nel grafo ha lunghezza pari.
Questo significa che possiamo dividere i vertici del grafo in due insiemi tali che ogni spigolo collega vertici appartenenti a insiemi diversi, e che se c'è un ciclo in questo grafo, deve avere un numero pari di spigoli.

