Un grafo con numero cromatico k è sempre detto k-partito?
No, sebbene il concetto di grafo k-partito e il numero cromatico $ \chi(G) $ di un grafo siano correlati, non sono equivalenti. Pertanto, non è corretto affermare che un grafo con un numero cromatico $ \chi(G) = k $ sia automaticamente classificabile come k-partito.
- Numero cromatico
Il numero cromatico di un grafo, denotato con \(\chi(G)\), è il minimo numero di colori necessari per colorare i vertici del grafo in modo tale che nessun due vertici adiacenti abbiano lo stesso colore. Il numero cromatico è una misura di quanto il grafo sia "complicato" dal punto di vista della colorazione dei vertici. - Grafo k-partito
Un grafo è detto k-partito se i suoi vertici possono essere divisi in k insiemi disgiunti, in modo tale che non esistano spigoli tra vertici dello stesso insieme. In particolare, un grafo bipartito è un caso speciale dove \(k=2\). L'attributo "k-partito" si riferisce alla struttura del grafo e alla maniera in cui i vertici possono essere separati in k insiemi indipendenti.
Ad esempio, un grafo con numero cromatico 3 necessita di 3 colori per una colorazione appropriata in cui vertici adiacenti hanno colori diversi, ma questo non implica che i vertici possano essere divisi in 3 insiemi con nessun spigolo interno a ciascun insieme.
Un grafo potrebbe avere una struttura che richiede almeno 3 colori per la colorazione, ma non soddisfa necessariamente le condizioni per essere considerato 3-partito. Un grafo è 3-partito se esiste una divisione dei suoi vertici in 3 insiemi disgiunti tali che gli spigoli connettono solo vertici di insiemi diversi.
Un esempio classico di un grafo con numero cromatico 3 che non è 3-partito è il grafo del triangolo, noto anche come C3 o ciclo su 3 vertici.
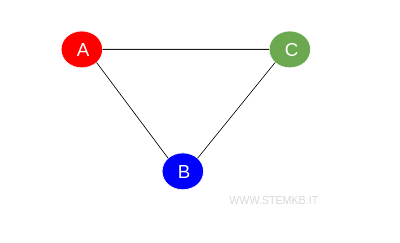
Nel grafo del triangolo ogni vertice è connesso con gli altri due, il che rende impossibile dividere i vertici in tre insiemi disgiunti.
Pertanto, un grafo con un numero cromatico di 3 potrebbe non essere 3-partito se non può essere diviso in tre insiemi disgiunti secondo la definizione di grafo k-partito.
Il grafo del triangolo è un chiaro esempi di un grafo che, nonostante abbia un numero cromatico di 3, non soddisfa i criteri per essere considerato 3-partito a causa della sua struttura intrinsecamente connessa.
Lo stesso vale per qualsiasi grafo k-partito e per qualsiasi numero cromatico.

