
Le grandezze vettoriali
Le grandezze vettoriali descrivono fenomeni che non possono essere caratterizzati semplicemente da un valore numerico (o modulo), ma richiedono anche un'indicazione della direzione e del verso.
Alcune grandezze fisiche, come la massa o il volume, si esprimono con un numero accompagnato da un’unità di misura.
Queste sono le grandezze scalari.
Ad esempio, la massa di un oggetto: \(7 \, \text{kg}\) o il volume di un recipiente: \(4 \, \text{litri}\)
Le grandezze scalari sono sufficienti quando non ci interessa conoscere altre caratteristiche, come la direzione di applicazione o movimento.
Tuttavia, ci sono situazioni in cui un numero da solo non basta.
Pensiamo a un esempio pratico: ci troviamo in una città sconosciuta e chiediamo indicazioni per trovare l'autostrada.

Una risposta come "l'autostrada è a mezzo chilometro" non è sufficiente, poiché non specifica "dove" si trova. Serve sapere anche la "direzione" (ad esempio, nord-ovest) e il "verso" (da dove partiamo a dove andiamo).
Per rispondere a queste domande dobbiamo usare delle grandezze vettoriali.
Cosa sono le grandezze vettoriali?
Le grandezze vettoriali sono quelle che richiedono tre elementi per essere completamente definite:
- Modulo: il valore numerico (sempre positivo) con un’unità di misura.
- Direzione: la linea lungo cui la grandezza agisce, rappresentata graficamente da una retta.
- Verso: l’orientamento lungo la direzione, indicato dalla punta di una freccia.
Sono dette grandezze "vettoriali" perché sono rappresentate da vettori.
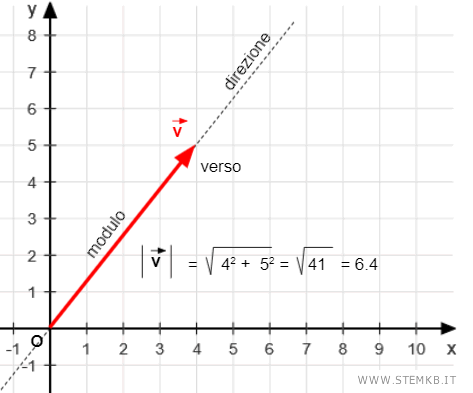
Un vettore è un ente matematico che rappresenta graficamente le grandezze vettoriali. Viene solitamente disegnato come una freccia:
- La lunghezza della freccia indica il modulo.
- La linea su cui si trova la freccia rappresenta la direzione.
- La punta della freccia mostra il verso.
Un esempio pratico è lo spostamento verso una città. Se ci troviamo in automobile con un navigatore GPS, sul display vediamo una freccia che ci mostra esattamente dove andare e quale è la distanza per raggiungere la nostra meta.

Le grandezze vettoriali possono essere combinate tramite operazioni come la somma e la sottrazione, seguendo regole specifiche:
Questi principi sono essenziali, ad esempio, per calcolare l’effetto complessivo di più forze su un corpo.
Un dettaglio importante: differenza tra direzione e verso. Spesso si confondono i termini direzione e verso, ma hanno significati distinti. La direzione è la linea lungo cui si svolge il fenomeno (es., la rotta Milano-Roma). Il verso, invece, specifica il punto di partenza e quello di arrivo (da Milano verso Roma, o viceversa).
In conclusione, le grandezze vettoriali sono molto utili perché ci permettono di descrivere il mondo fisico con maggiore precisione rispetto alle grandezze scalari.
Rappresentano fenomeni complessi come lo spostamento, la velocità e le forze, elementi fondamentali nello studio della fisica.

