La direzione del vettore

La direzione di un vettore può essere espressa come l'ampiezza di un angolo \( \alpha \) formato tra il vettore e l'asse reale positivo, cioè l'asse \( x \) in un sistema di riferimento cartesiano.

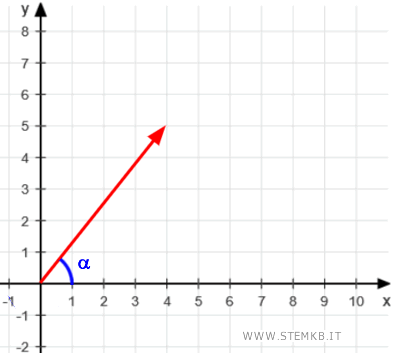
Per calcolarlo, possiamo sfruttare una relazione geometrica ben nota: la tangente di un angolo in un triangolo rettangolo.

Un vettore \( \vec{v} \) può essere descritto dalle sue componenti \( x \) e \( y \).

Se lo rappresentiamo su un piano cartesiano, possiamo immaginarlo come la diagonale di un rettangolo formato dai cateti \( |x| \) e \( |y| \), dove i valori assoluti vengono utilizzati per considerare sempre lunghezze positive.

La relazione che lega l'angolo \( \alpha \), il cateto opposto (\( y \)) e quello adiacente (\( x \)) è data dalla formula:

$$ \tan \alpha = \frac{|y|}{|x|} $$

Quindi, per trovare l'angolo \( \alpha \), è sufficiente prendere l'inversa della funzione tangente, ossia l'arcotangente, che ci permette di passare dal rapporto tra i lati a un angolo espresso in radianti o gradi:

$$ \alpha = \arctan \left( \frac{|y|}{|x|} \right) $$

Questa formula ci dice che la direzione del vettore dipende esclusivamente dal rapporto tra le sue componenti.

È importante ricordarsi che \( \alpha \) sarà sempre un angolo acuto (compreso tra \( 0^\circ \) e \( 90^\circ \)) quando entrambe le componenti sono positive.

Tuttavia, come vedremo negli esempi, bisogna fare attenzione ai segni di \( x \) e \( y \) che determinano in quale quadrante del piano si trova il vettore perché potrebbero anche essere negative!

Quando una o entrambe le componenti sono negative, è necessario aggiustare l'angolo che otteniamo con l'arcotangente in base al quadrante del piano cartesiano.

La direzione di un vettore non solo definisce "verso dove" si dirige il vettore, ma rappresenta anche un elemento chiave nella descrizione di fenomeni che implicano movimento, forze o altre grandezze vettoriali. Un errore nel calcolo dell'angolo può comportare conseguenze significative, ad esempio interpretare male il moto di un corpo o un fenomeno naturale.

Esempio pratico

Supponiamo di avere un vettore con componenti \( x = 3 \) e \( y = 4 \). La direzione del vettore si calcola così:

Calcoliamo il rapporto \( \frac{|y|}{|x|} \):

$$ \frac{|y|}{|x|} = \frac{4}{3} \approx 1.333 $$

Applichiamo la funzione arcotangente:

$$ \alpha = \arctan(1.333) $$

Usando una calcolatrice o uno strumento matematico, troviamo che:

$$ \alpha \approx 53.13^\circ $$

Quindi, la direzione del vettore è circa 53.13 gradi rispetto all'asse \( x \).

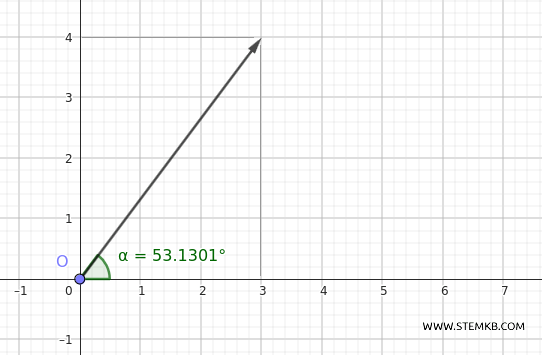
Determinare la direzione di un vettore utilizzando la tangente e l'arcotangente è un metodo semplice ed efficace, che mostra come la geometria e la trigonometria possano unirsi per descrivere fenomeni complessi.

Esempio 2

Facciamo un altro esempio.

Se le componenti del vettore sono \( x = -3 \) e \( y = 4 \), il calcolo della direzione del vettore cambia perché il segno delle componenti influisce sul quadrante in cui si trova il vettore nel piano cartesiano. Vediamo come procedere.

Anche in questo caso utilizziamo il valore assoluto delle componenti per calcolare il rapporto:

$$ \frac{|y|}{|x|} = \frac{4}{3} \approx 1.333 $$

L'angolo acuto \( \alpha \), formato con l'asse reale positivo, è dato da:

$$ \alpha = \arctan\left(\frac{|y|}{|x|}\right) = \arctan(1.333) $$

Usando una calcolatrice, troviamo:

$$ \alpha \approx 53.13^\circ $$

Poiché \( x = -3 \) (negativo) e \( y = 4 \) (positivo), il vettore si trova nel secondo quadrante del piano cartesiano.

In questo quadrante, la direzione del vettore è l'angolo misurato in senso antiorario a partire dall'asse \( x \) positivo, che corrisponde a:

$$ \theta = 180^\circ - \alpha $$

Sottraiamo l'angolo acuto \( \alpha \) da \( 180^\circ \):

$$ \theta = 180^\circ - 53.13^\circ \approx 126.87^\circ $$

Quindi, la direzione del vettore, tenendo conto delle componenti negative e positive, è:

$$ \theta \approx 126.87^\circ $$

Se disegniamo il vettore su un piano cartesiano, con \( x = -3 \) e \( y = 4 \), vediamo che punta verso il secondo quadrante.

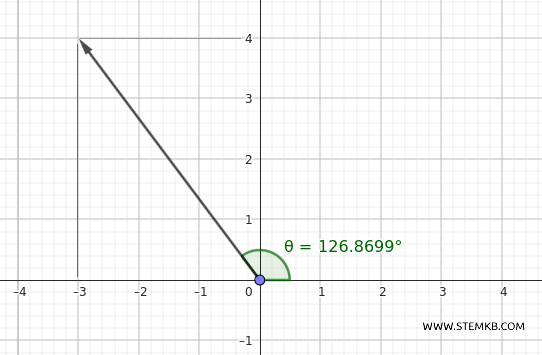
Il valore \( 126.87^\circ \) rappresenta l'angolo rispetto all'asse \( x \) positivo, come richiesto nelle convenzioni matematiche.

Questo dimostra che nel calcolo dell'angolo che definisce la direzione del vettore è molto importante capire in quale quadrante si trova il vettore.

Esempio 3

Se il vettore ha componenti \( x = -3 \) e \( y = -4 \), il calcolo della direzione cambia ancora, poiché il vettore si trova nel terzo quadrante del piano cartesiano.

Procediamo con i passaggi per determinare la direzione corretta.

Come prima, utilizziamo i valori assoluti delle componenti per calcolare il rapporto tra \( y \) e \( x \):

$$ \frac{|y|}{|x|} = \frac{4}{3} \approx 1.333 $$

L'angolo acuto \( \alpha \) formato rispetto all'asse reale positivo è dato da:

$$ \alpha = \arctan\left(\frac{|y|}{|x|}\right) = \arctan(1.333) $$

Usando una calcolatrice, troviamo:

$$ \alpha \approx 53.13^\circ $$

Poiché entrambe le componenti sono negative (\( x = -3 \) e \( y = -4 \)), il vettore si trova nel terzo quadrante.

In questo quadrante, la direzione del vettore è data da un angolo compreso tra \( 180^\circ \) e \( 270^\circ \).

Per calcolarlo, sommiamo l'angolo acuto \( \alpha \) a \( 180^\circ \), poiché stiamo misurando l'angolo in senso antiorario a partire dall'asse \( x \) positivo.

Sommiamo \( \alpha \) a \( 180^\circ \):

$$ \theta = 180^\circ + \alpha = 180^\circ + 53.13^\circ \approx 233.13^\circ $$

La direzione del vettore è:

$$ \theta \approx 233.13^\circ $$

Se disegniamo il vettore sul piano cartesiano, vedremo che l'angolo \( 233.13^\circ \) rappresenta la misura in senso antiorario a partire dall'asse \( x \) positivo.

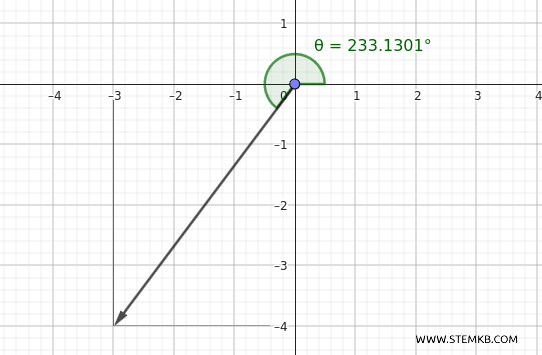
Esempio 4

Per completezza vediamo anche il caso in cui il vettore si trova nel quarto quadrante del piano cartesiano.

In questo caso il vettore ha componenti \( x = 3 \) e \( y = -4 \).

Calcoliamo il rapporto tra i valori assoluti delle componenti:

$$ \frac{|y|}{|x|} = \frac{4}{3} \approx 1.333 $$

L'angolo acuto \( \alpha \), formato rispetto all'asse reale positivo, è dato dall'arcotangente del rapporto

$$ \alpha = \arctan\left(\frac{|y|}{|x|}\right) = \arctan(1.333) $$

Usando una calcolatrice calcoliamo l'angolo

$$ \alpha \approx 53.13^\circ $$

Poiché \( x = 3 \) (positivo) e \( y = -4 \) (negativo), il vettore si trova nel quarto quadrante.

In questo caso, la direzione del vettore possiamo misurarla come un angolo negativo (al di sotto dell'asse \( x \) positivo) oppure come un angolo positivo maggiore di \( 270^\circ \), a seconda della convenzione.

Ad esempio, sottraiamo \( \alpha \) da \( 360^\circ \).

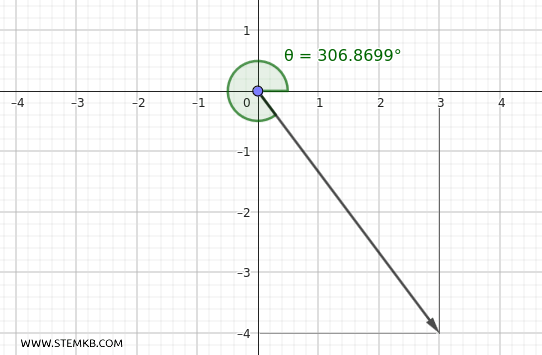
$$ \theta = 360^\circ - \alpha = 360^\circ - 53.13^\circ \approx 306.87^\circ $$

Quindi, la direzione del vettore è:

$$ \theta \approx 306.87^\circ $$

L'angolo \( 306.87^\circ \) è misurato in senso antiorario a partire dall'asse \( x \) positivo, e rappresenta la direzione del vettore.

Questi esercizi dimostrano chiaramente come il calcolo della direzione del vettore dipenda sia dalla tangente dell'angolo acuto sia dalla posizione del vettore nel piano cartesiano, determinata dai segni di \( x \) e \( y \).

Pertanto, ricorda... interpretare correttamente i quadranti è fondamentale per ottenere un angolo coerente con le convenzioni matematiche.