Il prodotto scalare tra due vettori
In questa lezione ti spiego cos'è e come si calcola il prodotto scalare di due vettori
Il prodotto scalare è un numero che si ottiene sommando i prodotti delle componenti di due vettori. $$ \vec{v_1} \cdot \vec{v_2} = x_1 \cdot x_2 + y_1 \cdot y_2 + z_1 \cdot z_2 $$ A volte il prodotto scalare lo trovi indicato anche con questa notazione $$ < \vec{v_1} , \vec{v_2} > = x_1 \cdot x_2 + y_1 \cdot y_2 + z_1 \cdot z_2 $$
Si chiama "scalare" perché il risultato è un numero, non è un vettore.
Ti faccio un esempio pratico.
Considera due vettori del piano.
$$ \vec{v_1} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} $$
$$ \vec{v_2} = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$
Ogni vettore ha due componenti x e y che corrispondono alle coordinate (x,y) sul piano.
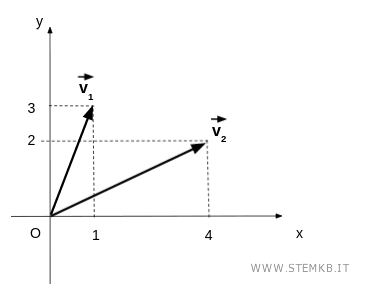
Il prodotto scalare tra i due vettori è la somma dei prodotti delle componenti.
$$ \vec{v_1} \cdot \vec{v_2} = x_1 \cdot x_2 + y_1 \cdot y_2 = 1 \cdot 4 + 3 \cdot 2 = 4+ 6 = 10 $$
Il prodotto scalare dei due vettori è il numero reale 10.
Quindi, il risultato non è un vettore ma un numero (scalare).
Nota In questo esempio ho usato due vettori sul piano. La procedura è la stessa anche se devi calcolare vettori con tre dimensioni (spazio) o più dimensioni. Ad esempio, per calcolare il prodotto scalare di due vettori nello spazio $$ \vec{v_1} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} $$ $$ \vec{v_2} = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} $$
devi sommare i prodotti delle loro componenti (x,y,z). $$ \vec{v_1} \cdot \vec{v_2} = x_1 \cdot x_2 + y_1 \cdot y_2 + z_1 \cdot z_2 $$ Il risultato è il prodotto scalare.
A cosa serve il prodotto scalare?
Il prodotto scalare tra due vettori è utile per capire l'ampiezza dell'angolo tra i due vettori
- Se il prodotto scalare è nullo, i due vettori formano un angolo di 90°. Quindi sono vettori perpendicolari oppure uno dei due vettori è nullo.
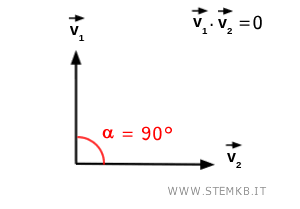
- Se il prodotto scalare è positivo, i due vettori formano un angolo minore di 90°.
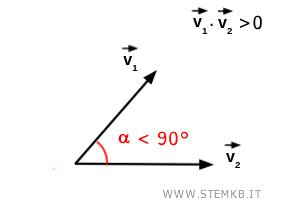
- Se il prodotto scalare è negativo, i due vettori formano un angolo maggiore di 90°.
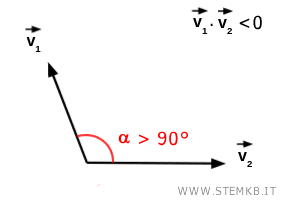
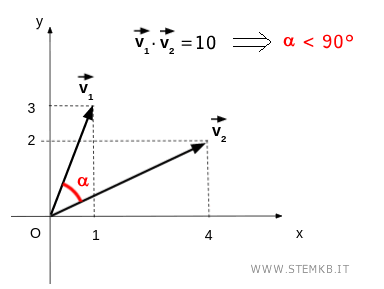
Nell'esempio precedente il prodotto scalare è positivo v1·v2=10.
Questo vuol dire che l'angolo più piccolo compreso tra i due vettori è minore di 90°.
La formula alternativa per calcolare il prodotto scalare
Per calcolare il prodotto scalare puoi anche moltiplicare i moduli (lunghezze) dei due vettori per il coseno dell'angolo alfa compreso tra i due vettori. $$ \vec{v_1} \cdot \vec{v_2} = |\vec{v_1} | \cdot |\vec{v_2} | \cdot \cos \alpha $$
E' una formula alternativa che ti permette di calcolare il prodotto scalare tra due vettori senza conoscere le componenti.
A seconda dei casi può essere conveniente usare l'una o altra.
Esempio
Nell'esempio precedente i due vettori formano un angolo di 45°.
Il primo vettore è lungo √10 mentre il secondo vettore √20
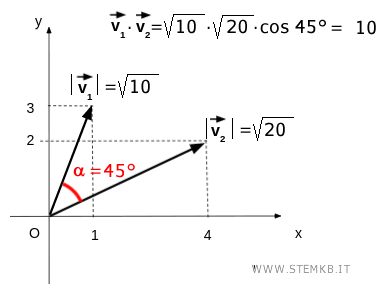
Il prodotto tra i moduli dei vettori e il coseno di 45° è uguale a 10.
$$ \vec{v_1} \cdot \vec{v_2} = |\vec{v_1} | \cdot |\vec{v_2} | \cdot \cos \alpha = \sqrt{10} \cdot \sqrt{20} \cdot \cos 45° = 10 $$
Il risultato del prodotto scalare è lo stesso.
Se questa lezione di algebra lineare ti piace, continua a seguirci.

