
La sottrazione dei vettori
La sottrazione tra due vettori è una operazione molto semplice ed è molto simile all'addizione.
Per calcolare la differenza tra due vettori, ti basta sottrarre le componenti corrispondenti di ciascun vettore.
Quindi, se hai due vettori v e w
$$ \vec{v} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} $$
la sottrazione v - w è definita come il vettore composto dalle differenze delle componenti
$$ \vec{v} - \vec{w} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} - \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} = \begin{pmatrix} v_1 - w_1 \\ v_2 - w_2 \\ \vdots \\ v_n - w_n \end{pmatrix} $$
Esempio. Considera due vettori $$ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} $$ $$ \vec{w} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ Il vettore differenza è un vettore composto dalle componenti del primo vettore meno quelle del secondo. $$ \vec{v} - \vec{w} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 3-1 \\ 4-2 \end{pmatrix} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$
Puoi considerae la sottrazione tra due vettori v e w come la somma di v con il vettore opposto di w.
Ecco un esempio pratico.
Se hai due vettori v e w
$$ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} $$ $$ \vec{w} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$
La sottrazione tra il primo vettore e il secondo è uguale alla somma del primo vettore e l'opposto del secondo vettore.
$$ \vec{v} - \vec{w} = \vec{v} + ( - \vec{w } ) $$
$$ \vec{v} - \vec{w} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} + ( - \begin{pmatrix} 1 \\ 2 \end{pmatrix} ) $$
$$ \vec{v} - \vec{w} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} + \begin{pmatrix} -1 \\ -2 \end{pmatrix} ) $$
$$ \vec{v} - \vec{w} = \begin{pmatrix} 3-1 \\ 4-2 \end{pmatrix} $$
$$ \vec{v} - \vec{w} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$
Dal punto di vista geometrico, la sottrazione di due vettori sl piano puoi ottenerla tracciando un vettore che congiunge il secondo vettore al primo vettore, traslato all'origine.
Ad esempio, rappresenta i vettori v=(3;4) e w=(1,2) dell'esempio precedente sul piano.
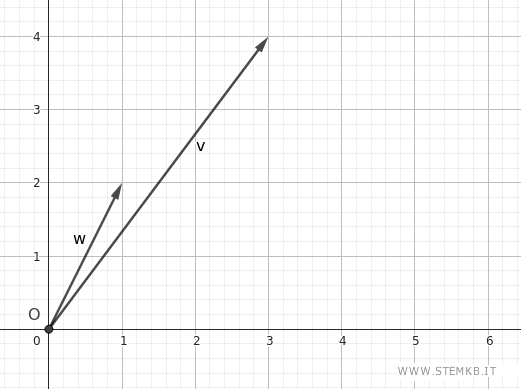
Per rappresentare la differenza v-w, traccia un vettore che congiunge il secondo vettore w (sottraendo) al primo vettore v (minuendo).
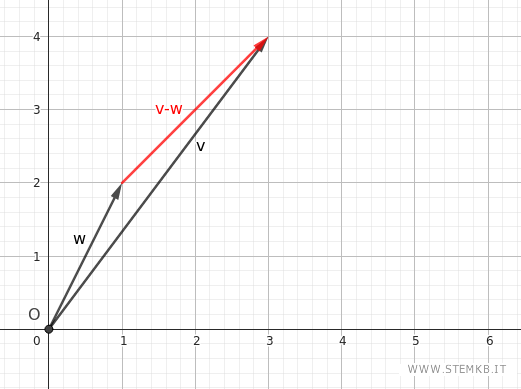
Poi trasla quest'ultimo vettore v-w per farlo partire dall'origine (O).
Il risultato finale è il vettore differenza.
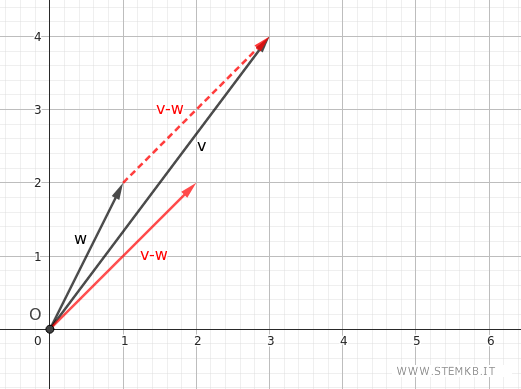
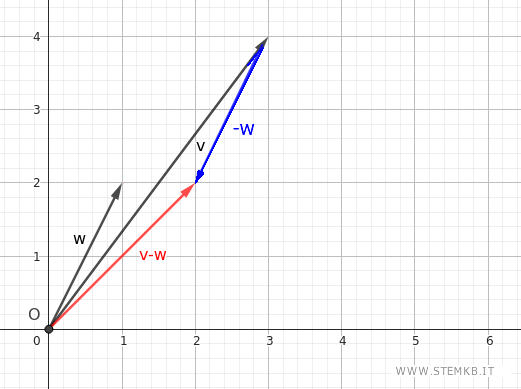
In alternativa, per sottrarre i vettori $ \vec{v} - \vec{w} $, puoi usare il metodo punta-coda sommando il vettore dividendo $ \vec{v} $ con il vettore opposto $ -\vec{w} $ del vettore divisore $ \vec{w} $.
Il risultato finale è sempre lo stesso.
Spero che queste informazioni siano utili. Se hai altre domande sui vettori, non esitare a chiedere.

